- 显著性物体不能均匀突出
- 卷积池化操作引起的信息丢失造成的轮廓不对
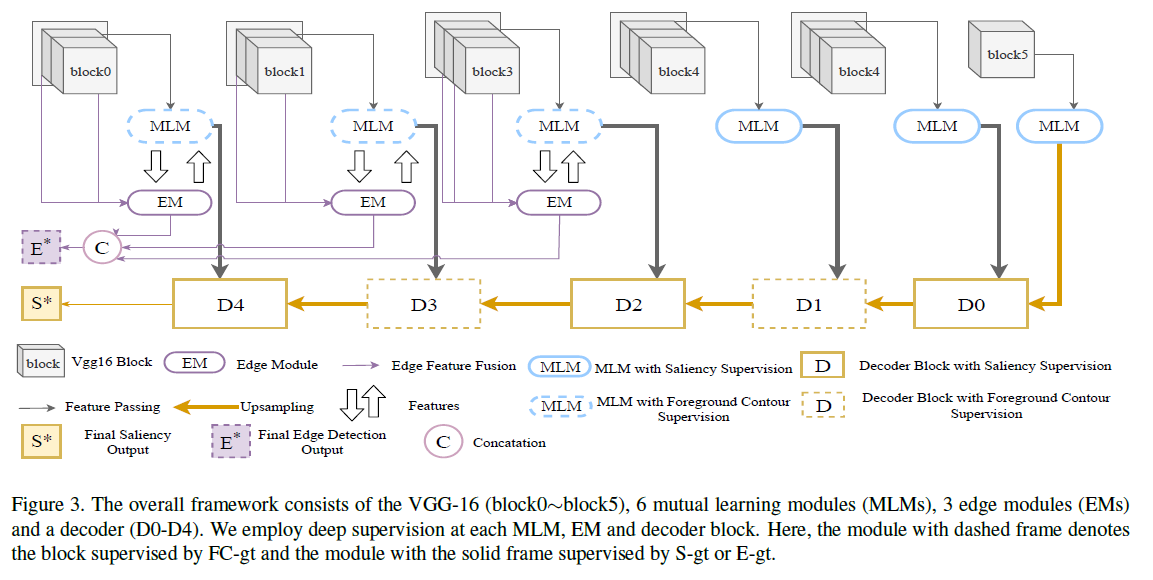可以看到是一个编码-解码的架构，编码部分使用了VGG-16的5个卷积块再加上最后一个池化层；解码部分则是融合不同的信息之后用反卷积进行上采样，同时每个解码器都用卷积生成了一个预测图
这部分主要是用于提高显著性检测和前景轮廓检测的性能
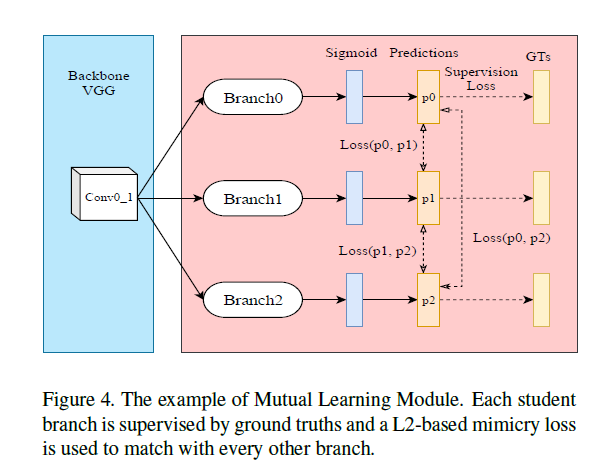$$
\left{\begin{array}{ll}{A_{s}^{i_{k}}=\operatorname{Sigmoid}\left(\phi_{s}^{i_{k}}\left(v_{i_{1}}\right)\right),} & {\text {for } i=0,1} \ {A_{s}^{i_{k}}=\operatorname{Sigmoid}\left(\phi_{s}^{i_{k}}\left(v_{i_{2}}\right)\right),} & {\text {for } i=2,3,4}\end{array}\right.
$$
$v_{i_{j}}$表示第$i$个卷积块的第$j$个卷积层的特征，$\phi_{s}^{i_{k}}$表示第$k$个子网络，当然$k$的值为1-3，这个互学习还是第一次见到，每个块的输出，相互监督，作者这里用了$L_2$监督学习，而$GT_S$的监督是分开的，前三层用了$fc-gt$(从$S-gt$中提取的前景轮廓。)，后三层用了$S-gt$(真值)监督。
作者提到在别人的研究中,对VGG-19预训练的模型进行微调，发现前3个卷积块的神经元响应不大（我也做过这样的实验，确实如此），而实验表明前三个块同时适用于边缘信息和显著性信息的捕获，因此作者在前三个卷积块的基础上加入边缘模块用于边缘检测，以此来帮助前景轮廓的检测
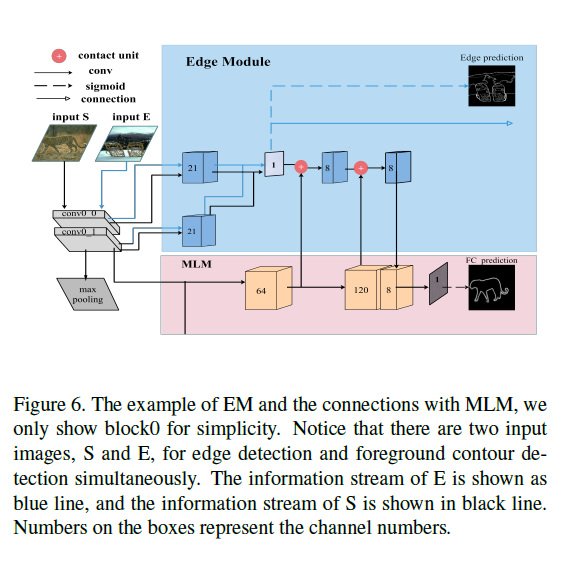将一个块中的每个卷积层连接到另一个卷积层，提取丰富的边缘特征，并将不同层的特征进行融合，生成边缘概率图。具体来说，对于输入图像$E$，每个$EM$生成一个边缘概率图$A_{e}^{i}$，并收集输出，融合到最终的边缘预测$E^{*}$中。对于输入图像$S$，$EM$只为$MLM$提供边缘特征映射$a_{e}^{i}$。这两个模块以残差的方式连接在一起，减少了用于前景轮廓检测的边缘特征中的噪声。
对于第$i$个块，表示$EM$的函数为$\psi^{i}$，输出特征图$a_{e}^{i}$和边缘特征图$A_{e}^{i}$可由下面的式子生成
$$
\left{\begin{array}{ll}{a_{e}^{i}=\psi^{i}\left(v_{i_{0}}, v_{i_{1}}\right),} & {\text { for } i=0,1} \ {a_{e}^{i}=\psi^{i}\left(v_{i_{0}}, v_{i_{1}}, v_{i_{2}}\right),} & {\text { for } \quad i=2} \ {A_{e}^{i}=\operatorname{Sigmoid}\left(a_{e}^{i}\right)} & {}\end{array}\right.
$$
这一部分看的我是一脸的懵逼，这些设计得脑洞多大啊！！
使用$FC-gt$作为较浅的三层模型的监督，以保持精细详细的轮廓信息，而$S-gt$作为较深的三个模块的监督，以关注语义信息。以一种交织的方式在不同的解码器块上交替应用两个任务。将$S-gt$设为$D_0、D_2、D_4$的监督，$FC-gt$设为$D_1、D_3$的监督。每个解码器块的目的是将前一个块的特征与相应的$MLM$融合，然后将特征传输到下一个块。
$D_1$在$FC-gt$的监督下，接收高层语义信息，并将其传输到前景轮廓特征中，剔除目标内部噪声，提取的轮廓特征变得更加清晰。$D_2$块是一种填充方案，它将轮廓特征提取出来，然后将其转化为显著特征。它需要根据轮廓特征检索内部信息，迫使$D_2$对轮廓内的每个像素产生统一的预测得分，就像一个填充过程。
然后将来自$D_2$的相对干净的语义信息和来自低层$MLM$轮廓信息发送到$D_3$块。$FC-gt$监督下的$D_3$块，其目的是利用高级语义知识，保持精确的前景轮廓，消除低层轮廓信息中多余的噪声。最后一块，$D_4$与$D_2$相似，在$S-gt$的监督下，试图基于前景信息填充显著性映射。
用了一些基本的损失函数，但是加了权重
$$
\mathcal{L}{E n c}=\theta{s} \mathcal{L}{S}+\theta{e} \mathcal{L}{E}+\theta{m} \mathcal{L}{\text {mimicry}}
$$
其中$\mathcal{L}{S}, \mathcal{L}{E}$和$\mathcal{L}{\text {mimicry}}$分别为$MLMs$中显著性任务的损失函数、边缘检测函数和互学习损失函数，$\theta_{\mathrm{S}}$为它们的权值，设为0.7、0.2、0.1。同样在解码器部分还有一个$bce$的损失函数，这个模型有很多的监督，基本每个块都有监督，但损失函数并不是平均分配的，文中给出了具体参数，却没有原因(估计是作者实验出来的吧)
- 从作者给出的视觉图来看，简直是个完美的模型啊，跟G&T差不多一样了
- 这个互学习，我觉得挺好的一个点，互相监督
- 在EM模块我是看蒙圈的，脑洞真大
- 模型用了两张图作为输入，这两张图好像是不一样的，因为来自不同的数据集，这不会造成干扰么？(单从作者给的结果来看，肯定是好的)
- 既然已经有了前景的轮廓了，却引入了另一张图，另一个边缘监督，边缘模块感觉多此一举了，但作者的结果给出这样确实是有效的，感觉有点那啥
- 文中基本出一个图，就有监督，感觉这会严重拖慢模型的速度呀
- 最后就是这个模型好像不是端到端的，分了三步去计算
