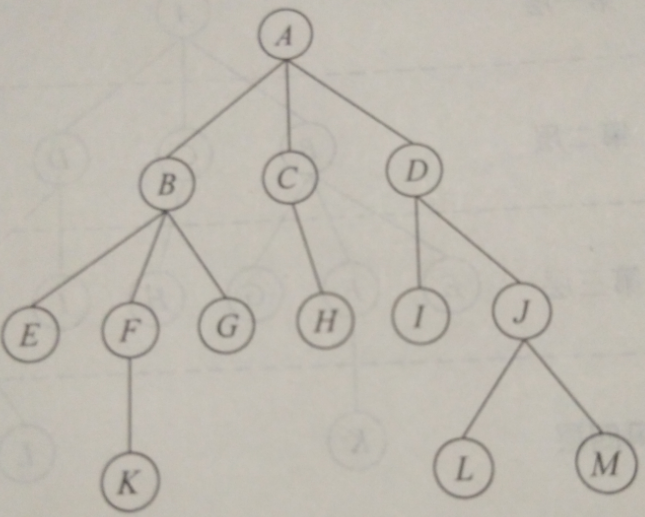
树是由n(n>=0)个结点组成的一个具有层次关系的有限集合.
# 空树和非空树
如果结点树n为0, 则该树是一棵空树, 否则是非空树.
# 结点
树中的每个元素称为结点.
# 根结点
在任意一棵非空树, 存在且仅存在一个根结点, 简称根, 根结点只有后继结点而没有前驱结点, 图中的A结点就是根结点.
# 子树
除根结点外, 其余结点可以分为多个互不相交的有限集合, 每个集合是一棵树, 称为根的子树,
如以B结点为根, 是一棵树, 以H结点为根, 是一棵树, 因此可以说树是由根结点和若干子树构成的.
# 子结点
在一棵树中, 每个结点的直接后继结点称为该结点的孩子结点(子结点), 相应地, 该结点称为子结点的双亲结点(父结点).
如, A是B C D的父结点, B C D是A结点的子结点.
# 兄弟结点
具有同一父结点的结点互为兄弟结点.
如, E F G是兄弟结点.
# 堂兄弟结点
隔代的兄弟结点称为堂兄弟结点.
如, E H I为堂兄弟结点.
# 子孙结点
具有垂直的直系关系.
如以B C D为根结点的子树上的所有结点都是A结点的子孙结点, A B F结点都是K结点的祖先结点.
# 结点的度
结点拥有的子树的数目称为结点的度.
如, A结点的度是3, 因为它有B C D三棵子树, C结点的度是1.
# 树的度
树中各个结点的度的最大值称为树的度, 通常将度为m的树称为m次树, 上图中的树是3次树, 因为结点度最大值为3.
# 非终端结点或分支结点
结点度不为0的结点, 如 B C D F结点.
# 终端结点或叶子结点
结点度为0的结点, 也就是没有后继结点的结点, 如E H K L结点.
# 树的高度或深度
根结点为第一层, 根结点的子节点为第二层, 以此类推, 树的最大层次为树的高度或深度.
如, 上图中的树有4层, 即树的高度为4.
# 森林
多棵树可以组成一个森林, 森林就是m(m>=0)棵互不相交的树的集合, 对于树来说, 其子树的集合就是森林.
如, 上图中的树, 删除根结点A之后, 其子树就组成了一个森林.
# 有序树和无序树
如果一棵树中的结点从左至右是有序的, 不能互换, 则称这棵树为有序树, 否则称为无序树.
若无特别指明, 一般讨论的都是有序树.
在有序树中, 最左边的子树称为第一个孩子, 最右边的子树称为最后一个孩子.
图形表示法是树结构最常用的表示法方法, 在树形图中, 结点用圆圈表示, 元素名称写在圆圈中,
各个结点之间的关系用连接线来表示, 这种方法直观、清晰、易于理解.
用广义表来表示树形结构时, 根结点写在最外层, 即表的最左边, 第一层是其子节点, 第二层是其孙子结点, 逐层深入.
如, 上图中的树用广义表来表示, 如下所示:
第一步先写出根结点及其子节点, (A(B,C,D))
第二步写出B C D结点的子节点, (A(B(E,F,G),C(H),D(I,J)))
第三步写出第三层结点的子节点, (A(B(E,F(K),G),C(H),D(I,J(L,M))))
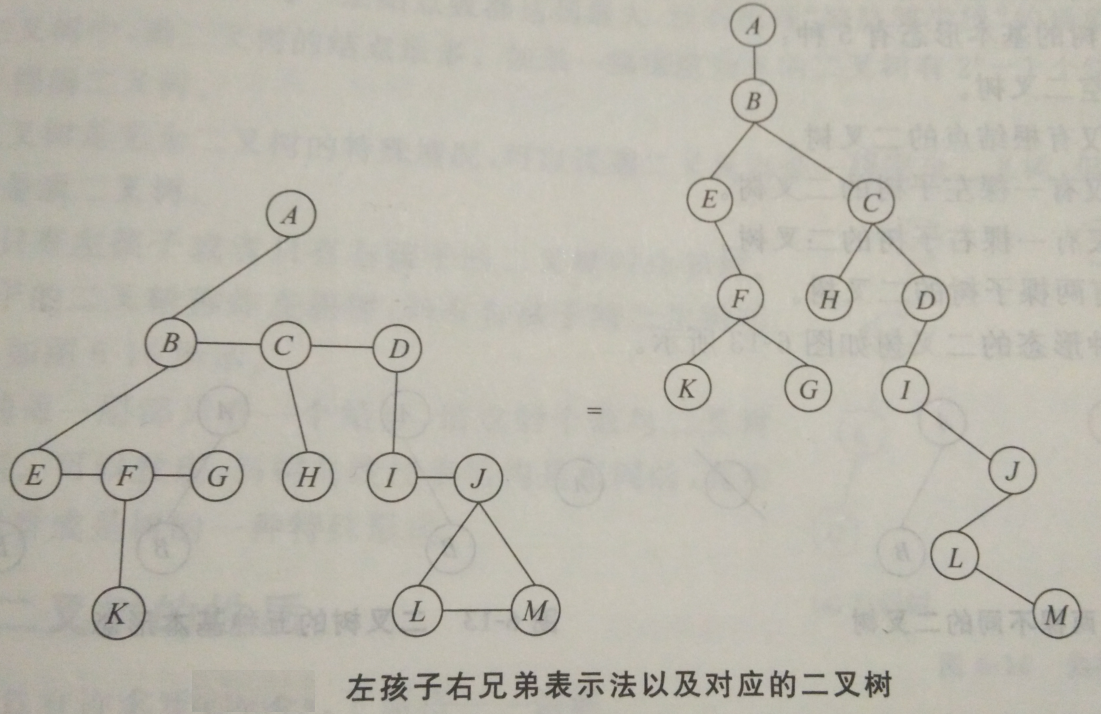
左孩子右兄弟表示法指的是由左边的子结点接管父结点其余的子节点.
上图中的树转换之后如下图所示, 并且, 左孩子右兄弟表示法可以将一棵多叉树转换为一棵二叉树.