forked from shunliz/Machine-Learning
-
Notifications
You must be signed in to change notification settings - Fork 0
/
rnn-bptt.md
90 lines (45 loc) · 7.42 KB
/
rnn-bptt.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
# 循环神经网络\(RNN\)模型与前向反向传播算法
---
在前面我们讲到了DNN,以及DNN的特例CNN的模型和前向反向传播算法,这些算法都是前向反馈的,模型的输出和模型本身没有关联关系。今天我们就讨论另一类输出和模型间有反馈的神经网络:循环神经网络\(Recurrent Neural Networks ,以下简称RNN\),它广泛的用于自然语言处理中的语音识别,手写书别以及机器翻译等领域。
# 1. RNN概述
在前面讲到的DNN和CNN中,训练样本的输入和输出是比较的确定的。但是有一类问题DNN和CNN不好解决,就是训练样本输入是连续的序列,且序列的长短不一,比如基于时间的序列:一段段连续的语音,一段段连续的手写文字。这些序列比较长,且长度不一,比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。
而对于这类问题,RNN则比较的擅长。那么RNN是怎么做到的呢?RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引$$\tau$$的。对于这其中的任意序列索引号t,它对应的输入是对应的样本序列中的$$x^{(t)}$$。而模型在序列索引号t位置的隐藏状态$$h^{(t)}$$,则由$$x^{(t)}$$和在t-1位置的隐藏状态$$h^{(t-1)}$$共同决定。在任意序列索引号t,我们也有对应的模型预测输出$$o^{(t)}$$。通过预测输出$$o^{(t)}$$和训练序列真实输出$$y^{(t)}$$,以及损失函数$$L^{(t)}$$,我们就可以用DNN类似的方法来训练模型,接着用来预测测试序列中的一些位置的输出。

下面我们来看看RNN的模型。
# 2. RNN模型
RNN模型有比较多的变种,这里介绍最主流的RNN模型结构如下:
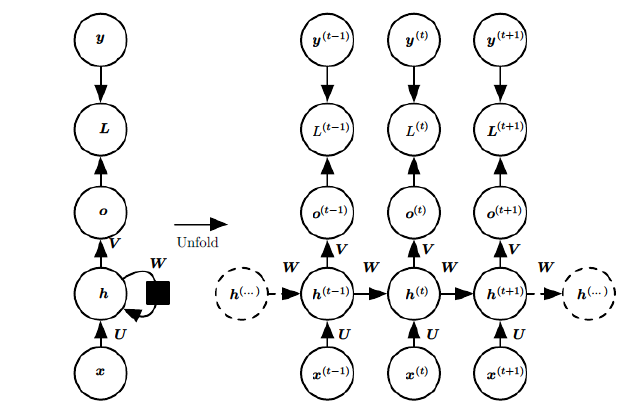
上图中左边是RNN模型没有按时间展开的图,如果按时间序列展开,则是上图中的右边部分。我们重点观察右边部分的图。
这幅图描述了在序列索引号t附近RNN的模型。其中:
1)$$x^{(t)}$$代表在序列索引号t时训练样本的输入。同样的,$$x^{(t-1)}$$和$$x^{(t+1)}$$代表在序列索引号t-1和t+1时训练样本的输入。
2)$$h^{(t)}$$代表在序列索引号t时模型的隐藏状态。$$h^{(t)}$$由$$x^{(t)}$$和$$h^{(t-1)}$$共同决定。
3)$$o^{(t)}$$代表在序列索引号t时模型的输出。$$o^{(t)}$$只由模型当前的隐藏状态$$h^{(t)}$$决定。
4)$$L^{(t)}$$代表在序列索引号t时模型的损失函数。
5)$$y^{(t)}$$代表在序列索引号t时训练样本序列的真实输出。
6)U,W,V这三个矩阵是我们的模型的线性关系参数,它在整个RNN网络中是共享的,这点和DNN很不相同。 也正因为是共享了,它体现了RNN的模型的“循环反馈”的思想。
# 3. RNN前向传播算法
有了上面的模型,RNN的前向传播算法就很容易得到了。
对于任意一个序列索引号t,我们隐藏状态$$h^{(t)}$$由$$x^{(t)}$$和$$h^{(t-1)}$$得到:$$h^{(t)} = \sigma(z^{(t)}) = \sigma(Ux^{(t)} + Wh^{(t-1)} +b)$$
其中$$\sigma$$为RNN的激活函数,一般为tanh,b为线性关系的偏倚。
序列索引号t时模型的输出$$o^{(t)}$$的表达式比较简单:$$o^{(t)} = Vh^{(t)} +c$$
在最终在序列索引号t时我们的预测输出为:$$\hat{y}^{(t)} = \sigma(o^{(t)})$$
通常由于RNN是识别类的分类模型,所以上面这个激活函数一般是softmax。
通过损失函数$$L^{(t)}$$,比如对数似然损失函数,我们可以量化模型在当前位置的损失,即$$\hat{y}^{(t)}$$和$$y^{(t)}$$的差距。
# 4. RNN反向传播算法推导
有了RNN前向传播算法的基础,就容易推导出RNN反向传播算法的流程了。RNN反向传播算法的思路和DNN是一样的,即通过梯度下降法一轮轮的迭代,得到合适的RNN模型参数U,W,V,b,c。由于我们是基于时间反向传播,所以RNN的反向传播有时也叫做BPTT\(back-propagation through time\)。当然这里的BPTT和DNN也有很大的不同点,即这里所有的U,W,V,b,c在序列的各个位置是共享的,反向传播时我们更新的是相同的参数。
为了简化描述,这里的损失函数我们为对数损失函数,输出的激活函数为softmax函数,隐藏层的激活函数为tanh函数。
对于RNN,由于我们在序列的每个位置都有损失函数,因此最终的损失L为:$$L = \sum\limits_{t=1}^{\tau}L^{(t)}$$
其中V,c,的梯度计算是比较简单的:
$$\frac{\partial L}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)}$$
$$\frac{\partial L}{\partial V} =\sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}(\hat{y}^{(t)} -y^{(t)}) (h^{(t)})^T$$
但是W,U,b的梯度计算就比较的复杂了。从RNN的模型可以看出,在反向传播时,在在某一序列位置t的梯度损失由当前位置的输出对应的梯度损失和序列索引位置t+1时的梯度损失两部分共同决定。对于W在某一序列位置t的梯度损失需要反向传播一步步的计算。我们定义序列索引t位置的隐藏状态的梯度为:$$\delta^{(t)} = \frac{\partial L}{\partial h^{(t)}}$$
这样我们可以像DNN一样从$$\delta^{(t+1)}$$递推$$\delta^{(t)}$$。$$\delta^{(t)} =\frac{\partial L}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}} = V^T(\hat{y}^{(t)} - y^{(t)}) + W^T\delta^{(t+1)}diag(1-(h^{(t+1)})^2)$$
对于$$\delta^{(\tau)}$$,由于它的后面没有其他的序列索引了,因此有:$$\delta^{(\tau)} =\frac{\partial L}{\partial o^{(\tau)}} \frac{\partial o^{(\tau)}}{\partial h^{(\tau)}} = V^T(\hat{y}^{(\tau)} - y^{(\tau)})$$
有了$$\delta^{(t)}$$,计算W,U,b就容易了,这里给出W,U,b的梯度计算表达式:
$$\frac{\partial L}{\partial W} = \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial W} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}(h^{(t-1)})^T$$
$$\frac{\partial L}{\partial b}= \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial b} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}$$
$$\frac{\partial L}{\partial U} = \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial U} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}(x^{(t)})^T$$
除了梯度表达式不同,RNN的反向传播算法和DNN区别不大,因此这里就不再重复总结了。
# 5. RNN小结
上面总结了通用的RNN模型和前向反向传播算法。当然,有些RNN模型会有些不同,自然前向反向传播的公式会有些不一样,但是原理基本类似。
RNN虽然理论上可以很漂亮的解决序列数据的训练,但是它也像DNN一样有梯度消失时的问题,当序列很长的时候问题尤其严重。因此,上面的RNN模型一般不能直接用于应用领域。在语音识别,手写书别以及机器翻译等NLP领域实际应用比较广泛的是基于RNN模型的一个特例LSTM,下一篇我们就来讨论LSTM模型。