forked from shunliz/Machine-Learning
-
Notifications
You must be signed in to change notification settings - Fork 0
/
scikit-lda.md
92 lines (61 loc) · 4.51 KB
/
scikit-lda.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
# 用scikit-learn进行LDA降维
---
在[线性判别分析LDA原理总结](/ml/clean-feature/xian-xing-pan-bie-fen-xi-lda.md)中,我们对LDA降维的原理做了总结,这里我们就对scikit-learn中LDA的降维使用做一个总结。
# 1. 对scikit-learn中LDA类概述
在scikit-learn中, LDA类是sklearn.discriminant\_analysis.LinearDiscriminantAnalysis。那既可以用于分类又可以用于降维。当然,应用场景最多的还是降维。和PCA类似,LDA降维基本也不用调参,只需要指定降维到的维数即可。
# 2. LinearDiscriminantAnalysis类概述
我们这里对LinearDiscriminantAnalysis类的参数做一个基本的总结。
1)**solver** : 即求LDA超平面特征矩阵使用的方法。可以选择的方法有奇异值分解"svd",最小二乘"lsqr"和特征分解"eigen"。一般来说特征数非常多的时候推荐使用svd,而特征数不多的时候推荐使用eigen。主要注意的是,如果使用svd,则不能指定正则化参数**shrinkage**进行正则化。默认值是svd
2)**shrinkage**:正则化参数,可以增强LDA分类的泛化能力。如果仅仅只是为了降维,则一般可以忽略这个参数。默认是None,即不进行正则化。可以选择"auto",让算法自己决定是否正则化。当然我们也可以选择不同的\[0,1\]之间的值进行交叉验证调参。注意shrinkage只在solver为最小二乘"lsqr"和特征分解"eigen"时有效。
3)**priors** :类别权重,可以在做分类模型时指定不同类别的权重,进而影响分类模型建立。降维时一般不需要关注这个参数。
4)**n\_components**:即我们进行LDA降维时降到的维数。在降维时需要输入这个参数。注意只能为\[1,类别数-1\)范围之间的整数。如果我们不是用于降维,则这个值可以用默认的None。
从上面的描述可以看出,如果我们只是为了降维,则只需要输入n\_components,注意这个值必须小于“类别数-1”。PCA没有这个限制。
# 3. LinearDiscriminantAnalysis降维实例
在LDA的原理篇我们讲到,PCA和LDA都可以用于降维。两者没有绝对的优劣之分,使用两者的原则实际取决于数据的分布。由于LDA可以利用类别信息,因此某些时候比完全无监督的PCA会更好。下面我们举一个LDA降维可能更优的例子。
我们首先生成三类三维特征的数据,代码如下:
```
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
from sklearn.datasets.samples_generator import make_classification
X, y = make_classification(n_samples=1000, n_features=3, n_redundant=0, n_classes=3, n_informative=2,
n_clusters_per_class=1,class_sep =0.5, random_state =10)
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
plt.scatter(X[:, 0], X[:, 1], X[:, 2],marker='o',c=y)
```
我们看看最初的三维数据的分布情况:
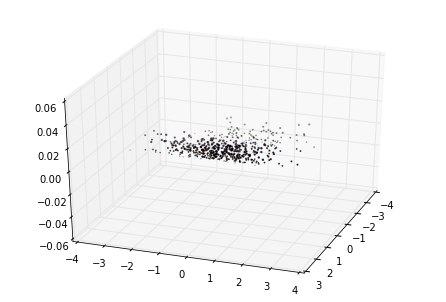
首先我们看看使用PCA降维到二维的情况,注意PCA无法使用类别信息来降维,代码如下:
```
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
print pca.explained_variance_ratio_
print pca.explained_variance_
X_new = pca.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=y)
plt.show()
```
在输出中,PCA找到的两个主成分方差比和方差如下:
```
[ 0.43377069 0.3716351 ]
[ 1.20962365 1.03635081]
```
输出的降维效果图如下:
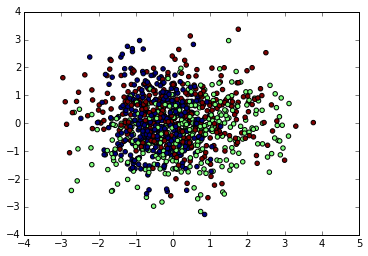
由于PCA没有利用类别信息,我们可以看到降维后,样本特征和类别的信息关联几乎完全丢失。
现在我们再看看使用LDA的效果,代码如下:
```
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X,y)
X_new = lda.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=y)
plt.show()
```
输出的效果图如下:
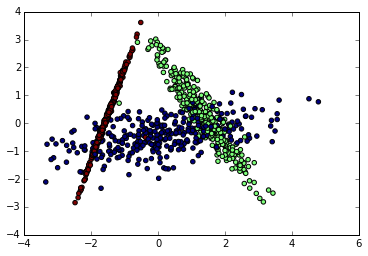
可以看出降维后样本特征和类别信息之间的关系得以保留。
一般来说,如果我们的数据是有类别标签的,那么优先选择LDA去尝试降维;当然也可以使用PCA做很小幅度的降维去消去噪声,然后再使用LDA降维。如果没有类别标签,那么肯定PCA是最先考虑的一个选择了。