欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
看完这篇文章虽然不能打十个,但是可以迅速打八个!而且够快!
学会二叉树的层序遍历,可以一口气撸完leetcode上八道题目:
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的前序遍历
- 515.在每个树行中找最大值
-
- 填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
题目地址:https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
思路:
我们之前讲过了三篇关于二叉树的深度优先遍历的文章:
接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:
这样就实现了层序从左到右遍历二叉树。
代码如下:这份代码也可以作为二叉树层序遍历的模板,以后再打七个就靠它了。
C++代码:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
};
python代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
quene = [root]
out_list = []
while quene:
length = len(queue) # 这里一定要先求出队列的长度,不能用range(len(queue)),因为queue长度是变化的
in_list = []
for _ in range(length):
curnode = queue.pop(0) # (默认移除列表最后一个元素)这里需要移除队列最头上的那个
in_list.append(curnode.val)
if curnode.left: queue.append(curnode.left)
if curnode.right: queue.append(curnode.right)
out_list.append(in_list)
return out_listjavascript代码:
var levelOrder = function(root) {
//二叉树的层序遍历
let res=[],queue=[];
queue.push(root);
if(root===null){
return res;
}
while(queue.length!==0){
// 记录当前层级节点数
let length=queue.length;
//存放每一层的节点
let curLevel=[];
for(let i=0;i<length;i++){
let node=queue.shift();
curLevel.push(node.val);
// 存放当前层下一层的节点
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curLevel);
}
return res;
};此时我们就掌握了二叉树的层序遍历了,那么如下五道leetcode上的题目,只需要修改模板的一两行代码(不能再多了),便可打倒!
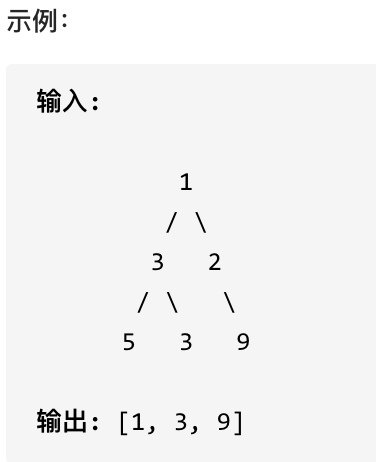
题目链接:https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
思路:
相对于102.二叉树的层序遍历,就是最后把result数组反转一下就可以了。
C++代码:
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
reverse(result.begin(), result.end()); // 在这里反转一下数组即可
return result;
}
};python代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
quene = [root]
out_list = []
while quene:
in_list = []
for _ in range(len(quene)):
node = quene.pop(0)
in_list.append(node.val)
if node.left:
quene.append(node.left)
if node.right:
quene.append(node.right)
out_list.append(in_list)
out_list.reverse()
return out_list
# 执行用时:36 ms, 在所有 Python3 提交中击败了92.00%的用户
# 内存消耗:15.2 MB, 在所有 Python3 提交中击败了63.76%的用户javascript代码
var levelOrderBottom = function(root) {
let res=[],queue=[];
queue.push(root);
while(queue.length&&root!==null){
// 存放当前层级节点数组
let curLevel=[];
// 计算当前层级节点数量
let length=queue.length;
while(length--){
let node=queue.shift();
// 把当前层节点存入curLevel数组
curLevel.push(node.val);
// 把下一层级的左右节点存入queue队列
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
}
res.push(curLevel);
}
return res.reverse();
};题目链接:https://leetcode-cn.com/problems/binary-tree-right-side-view/
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
思路:
层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
C++代码:
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<int> result;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (i == (size - 1)) result.push_back(node->val); // 将每一层的最后元素放入result数组中
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};python代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if not root:
return []
# deque来自collections模块,不在力扣平台时,需要手动写入
# 'from collections import deque' 导入
# deque相比list的好处是,list的pop(0)是O(n)复杂度,deque的popleft()是O(1)复杂度
quene = deque([root])
out_list = []
while quene:
# 每次都取最后一个node就可以了
node = quene[-1]
out_list.append(node.val)
# 执行这个遍历的目的是获取下一层所有的node
for _ in range(len(quene)):
node = quene.popleft()
if node.left:
quene.append(node.left)
if node.right:
quene.append(node.right)
return out_list
# 执行用时:36 ms, 在所有 Python3 提交中击败了89.47%的用户
# 内存消耗:14.6 MB, 在所有 Python3 提交中击败了96.65%的用户javascript代码:
var rightSideView = function(root) {
//二叉树右视图 只需要把每一层最后一个节点存储到res数组
let res=[],queue=[];
queue.push(root);
while(queue.length&&root!==null){
// 记录当前层级节点个数
let length=queue.length;
while(length--){
let node=queue.shift();
//length长度为0的时候表明到了层级最后一个节点
if(!length){
res.push(node.val);
}
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
}
}
return res;
};题目链接:https://leetcode-cn.com/problems/average-of-levels-in-binary-tree/
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
思路:
本题就是层序遍历的时候把一层求个总和在取一个均值。
C++代码:
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<double> result;
while (!que.empty()) {
int size = que.size();
double sum = 0; // 统计每一层的和
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
sum += node->val;
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(sum / size); // 将每一层均值放进结果集
}
return result;
}
};
python代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: TreeNode) -> List[float]:
if not root:
return []
quene = deque([root])
out_list = []
while quene:
in_list = []
for _ in range(len(quene)):
node = quene.popleft()
in_list.append(node.val)
if node.left:
quene.append(node.left)
if node.right:
quene.append(node.right)
out_list.append(in_list)
out_list = map(lambda x: sum(x) / len(x), out_list)
return out_list
# 执行用时:56 ms, 在所有 Python3 提交中击败了81.48%的用户
# 内存消耗:17 MB, 在所有 Python3 提交中击败了89.68%的用户javascript代码:
var averageOfLevels = function(root) {
//层级平均值
let res=[],queue=[];
queue.push(root);
while(queue.length&&root!==null){
//每一层节点个数
let length=queue.length;
//sum记录每一层的和
let sum=0;
for(let i=0;i<length;i++){
let node=queue.shift();
sum+=node.val;
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
}
//每一层的平均值存入数组res
res.push(sum/length);
}
return res;
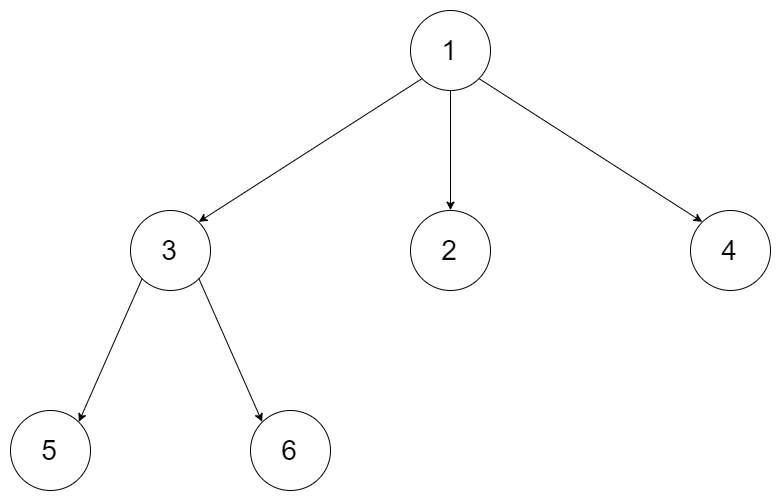
};题目链接:https://leetcode-cn.com/problems/n-ary-tree-level-order-traversal/
给定一个 N 叉树,返回其节点值的层序遍历。 (即从左到右,逐层遍历)。
例如,给定一个 3叉树 :
返回其层序遍历:
[ [1], [3,2,4], [5,6] ]
思路:
这道题依旧是模板题,只不过一个节点有多个孩子了
C++代码:
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
for (int i = 0; i < size; i++) {
Node* node = que.front();
que.pop();
vec.push_back(node->val);
for (int i = 0; i < node->children.size(); i++) { // 将节点孩子加入队列
if (node->children[i]) que.push(node->children[i]);
}
}
result.push_back(vec);
}
return result;
}
};python代码:
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if not root:
return []
quene = deque([root])
out_list = []
while quene:
in_list = []
for _ in range(len(quene)):
node = quene.popleft()
in_list.append(node.val)
if node.children:
# 这个地方要用extend而不是append,我们看下面的例子:
# In [18]: alist=[]
# In [19]: alist.append([1,2,3])
# In [20]: alist
# Out[20]: [[1, 2, 3]]
# In [21]: alist.extend([4,5,6])
# In [22]: alist
# Out[22]: [[1, 2, 3], 4, 5, 6]
# 可以看到extend对要添加的list进行了一个解包操作
# print(root.children),可以得到children是一个包含
# 孩子节点地址的list,我们使用for遍历quene的时候,
# 希望quene是一个单层list,所以要用extend
# 使用extend的情况,如果print(quene),结果是
# deque([<__main__.Node object at 0x7f60763ae0a0>])
# deque([<__main__.Node object at 0x7f607636e6d0>, <__main__.Node object at 0x7f607636e130>, <__main__.Node object at 0x7f607636e310>])
# deque([<__main__.Node object at 0x7f607636e880>, <__main__.Node object at 0x7f607636ef10>])
# 可以看到是单层list
# 如果使用append,print(quene)的结果是
# deque([<__main__.Node object at 0x7f18907530a0>])
# deque([[<__main__.Node object at 0x7f18907136d0>, <__main__.Node object at 0x7f1890713130>, <__main__.Node object at 0x7f1890713310>]])
# 可以看到是两层list,这样for的遍历就会报错
quene.extend(node.children)
out_list.append(in_list)
return out_list
# 执行用时:60 ms, 在所有 Python3 提交中击败了76.99%的用户
# 内存消耗:16.5 MB, 在所有 Python3 提交中击败了89.19%的用户JavaScript代码:
var levelOrder = function(root) {
//每一层可能有2个以上,所以不再使用node.left node.right
let res=[],queue=[];
queue.push(root);
while(queue.length&&root!==null){
//记录每一层节点个数还是和二叉树一致
let length=queue.length;
//存放每层节点 也和二叉树一致
let curLevel=[];
while(length--){
let node = queue.shift();
curLevel.push(node.val);
//这里不再是 ndoe.left node.right 而是循坏node.children
for(let item of node.children){
item&&queue.push(item);
}
}
res.push(curLevel);
}
return res;
};题目链接:https://leetcode-cn.com/problems/find-largest-value-in-each-tree-row/
您需要在二叉树的每一行中找到最大的值。
思路:
层序遍历,取每一层的最大值
C++代码:
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<int> result;
while (!que.empty()) {
int size = que.size();
int maxValue = INT_MIN; // 取每一层的最大值
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
maxValue = node->val > maxValue ? node->val : maxValue;
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(maxValue); // 把最大值放进数组
}
return result;
}
};javascript代码:
var largestValues = function(root) {
//使用层序遍历
let res=[],queue=[];
queue.push(root);
while(root!==null&&queue.length){
//设置max初始值就是队列的第一个元素
let max=queue[0];
let length=queue.length;
while(length--){
let node = queue.shift();
max=max>node.val?max:node.val;
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
}
//把每一层的最大值放到res数组
res.push(max);
}
return res;
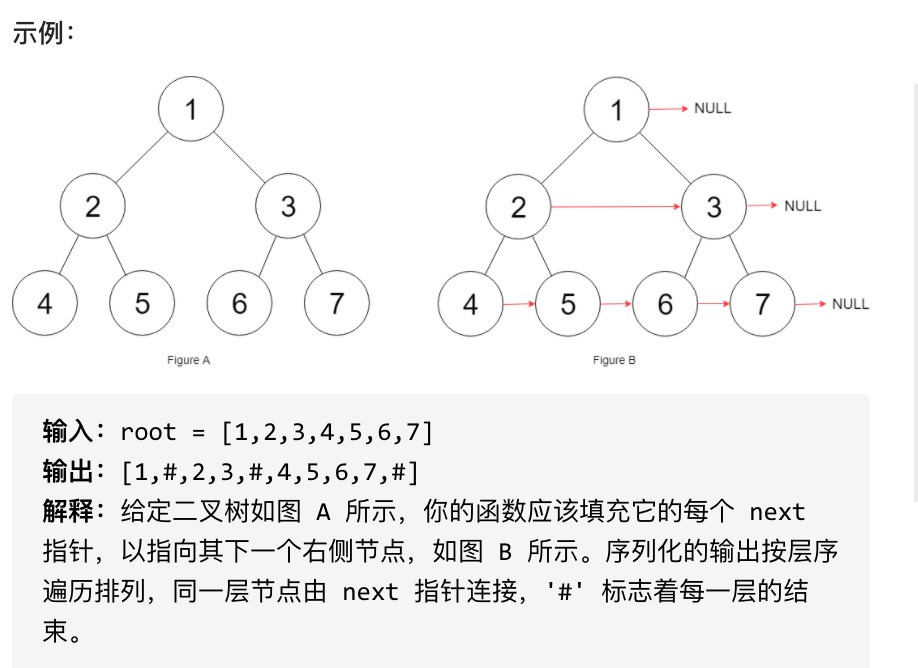
};题目链接:https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/
给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
思路:
本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
C++代码:
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
vector<int> vec;
Node* nodePre;
Node* node;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = que.front(); // 取出一层的头结点
que.pop();
node = nodePre;
} else {
node = que.front();
que.pop();
nodePre->next = node; // 本层前一个节点next指向本节点
nodePre = nodePre->next;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
nodePre->next = NULL; // 本层最后一个节点指向NULL
}
return root;
}
};题目地址:https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii/
思路:
这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
C++代码:
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
vector<int> vec;
Node* nodePre;
Node* node;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = que.front(); // 取出一层的头结点
que.pop();
node = nodePre;
} else {
node = que.front();
que.pop();
nodePre->next = node; // 本层前一个节点next指向本节点
nodePre = nodePre->next;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
nodePre->next = NULL; // 本层最后一个节点指向NULL
}
return root;
}
};二叉树的层序遍历,就是图论中的广度优先搜索在二叉树中的应用,需要借助队列来实现(此时是不是又发现队列的应用了)。
虽然不能一口气打十个,打八个也还行。
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的前序遍历
- 515.在每个树行中找最大值
-
- 填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
如果非要打十个,还得找叶师傅!
Java:
// 102.二叉树的层序遍历
class Solution {
public List<List<Integer>> resList = new ArrayList<List<Integer>>();
public List<List<Integer>> levelOrder(TreeNode root) {
//checkFun01(root,0);
checkFun02(root);
return resList;
}
//DFS--递归方式
public void checkFun01(TreeNode node, Integer deep) {
if (node == null) return;
deep++;
if (resList.size() < deep) {
//当层级增加时,list的Item也增加,利用list的索引值进行层级界定
List<Integer> item = new ArrayList<Integer>();
resList.add(item);
}
resList.get(deep - 1).add(node.val);
checkFun01(node.left, deep);
checkFun01(node.right, deep);
}
//BFS--迭代方式--借助队列
public void checkFun02(TreeNode node) {
if (node == null) return;
Queue<TreeNode> que = new LinkedList<TreeNode>();
que.offer(node);
while (!que.isEmpty()) {
List<Integer> itemList = new ArrayList<Integer>();
int len = que.size();
while (len > 0) {
TreeNode tmpNode = que.poll();
itemList.add(tmpNode.val);
if (tmpNode.left != null) que.offer(tmpNode.left);
if (tmpNode.right != null) que.offer(tmpNode.right);
len--;
}
resList.add(itemList);
}
}
}
// 107. 二叉树的层序遍历 II
public class N0107 {
/**
* 解法:队列,迭代。
* 层序遍历,再翻转数组即可。
*/
public List<List<Integer>> solution1(TreeNode root) {
List<List<Integer>> list = new ArrayList<>();
Deque<TreeNode> que = new LinkedList<>();
if (root == null) {
return list;
}
que.offerLast(root);
while (!que.isEmpty()) {
List<Integer> levelList = new ArrayList<>();
int levelSize = que.size();
for (int i = 0; i < levelSize; i++) {
TreeNode peek = que.peekFirst();
levelList.add(que.pollFirst().val);
if (peek.left != null) {
que.offerLast(peek.left);
}
if (peek.right != null) {
que.offerLast(peek.right);
}
}
list.add(levelList);
}
List<List<Integer>> result = new ArrayList<>();
for (int i = list.size() - 1; i >= 0; i-- ) {
result.add(list.get(i));
}
return result;
}
}
// 199.二叉树的右视图
public class N0199 {
/**
* 解法:队列,迭代。
* 每次返回每层的最后一个字段即可。
*
* 小优化:每层右孩子先入队。代码略。
*/
public List<Integer> rightSideView(TreeNode root) {
List<Integer> list = new ArrayList<>();
Deque<TreeNode> que = new LinkedList<>();
if (root == null) {
return list;
}
que.offerLast(root);
while (!que.isEmpty()) {
int levelSize = que.size();
for (int i = 0; i < levelSize; i++) {
TreeNode poll = que.pollFirst();
if (poll.left != null) {
que.addLast(poll.left);
}
if (poll.right != null) {
que.addLast(poll.right);
}
if (i == levelSize - 1) {
list.add(poll.val);
}
}
}
return list;
}
}
// 637. 二叉树的层平均值
public class N0637 {
/**
* 解法:队列,迭代。
* 每次返回每层的最后一个字段即可。
*/
public List<Double> averageOfLevels(TreeNode root) {
List<Double> list = new ArrayList<>();
Deque<TreeNode> que = new LinkedList<>();
if (root == null) {
return list;
}
que.offerLast(root);
while (!que.isEmpty()) {
TreeNode peek = que.peekFirst();
int levelSize = que.size();
double levelSum = 0.0;
for (int i = 0; i < levelSize; i++) {
TreeNode poll = que.pollFirst();
levelSum += poll.val;
if (poll.left != null) {
que.addLast(poll.left);
}
if (poll.right != null) {
que.addLast(poll.right);
}
}
list.add(levelSum / levelSize);
}
return list;
}
}
// 429. N 叉树的层序遍历
public class N0429 {
/**
* 解法1:队列,迭代。
*/
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> list = new ArrayList<>();
Deque<Node> que = new LinkedList<>();
if (root == null) {
return list;
}
que.offerLast(root);
while (!que.isEmpty()) {
int levelSize = que.size();
List<Integer> levelList = new ArrayList<>();
for (int i = 0; i < levelSize; i++) {
Node poll = que.pollFirst();
levelList.add(poll.val);
List<Node> children = poll.children;
if (children == null || children.size() == 0) {
continue;
}
for (Node child : children) {
if (child != null) {
que.offerLast(child);
}
}
}
list.add(levelList);
}
return list;
}
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
}
}Python:
Go:
func levelOrder(root *TreeNode) [][]int {
result:=make([][]int,0)
if root==nil{
return result
}
queue:=make([]*TreeNode,0)
queue=append(queue,root)
for len(queue)>0{
list:=make([]int,0)
l:=len(queue)
for i:=0;i<l;i++{
level:=queue[0]
queue=queue[1:]
list=append(list,level.Val)
if level.Left!=nil{
queue=append(queue,level.Left)
}
if level.Right!=nil{
queue=append(queue,level.Right)
}
}
result=append(result,list)
}
return result
}二叉树的层序遍历(GO语言完全版)
/**
102. 二叉树的层序遍历
*/
func levelOrder(root *TreeNode) [][]int {
res:=[][]int{}
if root==nil{//防止为空
return res
}
queue:=list.New()
queue.PushBack(root)
var tmpArr []int
for queue.Len()>0 {
length:=queue.Len()//保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)//出队列
if node.Left!=nil{
queue.PushBack(node.Left)
}
if node.Right!=nil{
queue.PushBack(node.Right)
}
tmpArr=append(tmpArr,node.Val)//将值加入本层切片中
}
res=append(res,tmpArr)//放入结果集
tmpArr=[]int{}//清空层的数据
}
return res
}
/**
107. 二叉树的层序遍历 II
*/
func levelOrderBottom(root *TreeNode) [][]int {
queue:=list.New()
res:=[][]int{}
if root==nil{
return res
}
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()
tmp:=[]int{}
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)
if node.Left!=nil{
queue.PushBack(node.Left)
}
if node.Right!=nil{
queue.PushBack(node.Right)
}
tmp=append(tmp,node.Val)
}
res=append(res,tmp)
}
//反转结果集
for i:=0;i<len(res)/2;i++{
res[i],res[len(res)-i-1]=res[len(res)-i-1],res[i]
}
return res
}
/**
199. 二叉树的右视图
*/
func rightSideView(root *TreeNode) []int {
queue:=list.New()
res:=[][]int{}
var finaRes []int
if root==nil{
return finaRes
}
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()
tmp:=[]int{}
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)
if node.Left!=nil{
queue.PushBack(node.Left)
}
if node.Right!=nil{
queue.PushBack(node.Right)
}
tmp=append(tmp,node.Val)
}
res=append(res,tmp)
}
//取每一层的最后一个元素
for i:=0;i<len(res);i++{
finaRes=append(finaRes,res[i][len(res[i])-1])
}
return finaRes
}
/**
637. 二叉树的层平均值
*/
func averageOfLevels(root *TreeNode) []float64 {
res:=[][]int{}
var finRes []float64
if root==nil{//防止为空
return finRes
}
queue:=list.New()
queue.PushBack(root)
var tmpArr []int
for queue.Len()>0 {
length:=queue.Len()//保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)//出队列
if node.Left!=nil{
queue.PushBack(node.Left)
}
if node.Right!=nil{
queue.PushBack(node.Right)
}
tmpArr=append(tmpArr,node.Val)//将值加入本层切片中
}
res=append(res,tmpArr)//放入结果集
tmpArr=[]int{}//清空层的数据
}
//计算每层的平均值
length:=len(res)
for i:=0;i<length;i++{
var sum int
for j:=0;j<len(res[i]);j++{
sum+=res[i][j]
}
tmp:=float64(sum)/float64(len(res[i]))
finRes=append(finRes,tmp)//将平均值放入结果集合
}
return finRes
}
/**
429. N 叉树的层序遍历
*/
func levelOrder(root *Node) [][]int {
queue:=list.New()
res:=[][]int{}//结果集
if root==nil{
return res
}
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()//记录当前层的数量
var tmp []int
for T:=0;T<length;T++{//该层的每个元素:一添加到该层的结果集中;二找到该元素的下层元素加入到队列中,方便下次使用
myNode:=queue.Remove(queue.Front()).(*Node)
tmp=append(tmp,myNode.Val)
for i:=0;i<len(myNode.Children);i++{
queue.PushBack(myNode.Children[i])
}
}
res=append(res,tmp)
}
return res
}
/**
515. 在每个树行中找最大值
*/
func largestValues(root *TreeNode) []int {
res:=[][]int{}
var finRes []int
if root==nil{//防止为空
return finRes
}
queue:=list.New()
queue.PushBack(root)
var tmpArr []int
//层次遍历
for queue.Len()>0 {
length:=queue.Len()//保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)//出队列
if node.Left!=nil{
queue.PushBack(node.Left)
}
if node.Right!=nil{
queue.PushBack(node.Right)
}
tmpArr=append(tmpArr,node.Val)//将值加入本层切片中
}
res=append(res,tmpArr)//放入结果集
tmpArr=[]int{}//清空层的数据
}
//找到每层的最大值
for i:=0;i<len(res);i++{
finRes=append(finRes,max(res[i]...))
}
return finRes
}
func max(vals...int) int {
max:=int(math.Inf(-1))//负无穷
for _, val := range vals {
if val > max {
max = val
}
}
return max
}
/**
116. 填充每个节点的下一个右侧节点指针
117. 填充每个节点的下一个右侧节点指针 II
*/
func connect(root *Node) *Node {
res:=[][]*Node{}
if root==nil{//防止为空
return root
}
queue:=list.New()
queue.PushBack(root)
var tmpArr []*Node
for queue.Len()>0 {
length:=queue.Len()//保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*Node)//出队列
if node.Left!=nil{
queue.PushBack(node.Left)
}
if node.Right!=nil{
queue.PushBack(node.Right)
}
tmpArr=append(tmpArr,node)//将值加入本层切片中
}
res=append(res,tmpArr)//放入结果集
tmpArr=[]*Node{}//清空层的数据
}
//遍历每层元素,指定next
for i:=0;i<len(res);i++{
for j:=0;j<len(res[i])-1;j++{
res[i][j].Next=res[i][j+1]
}
}
return root
}Javascript:
var levelOrder = function (root) {
let ans = [];
if (!root) return ans;
let queue = [root];
while (queue.length) {
let size = queue.length;
let temp = [];
while (size--) {
let n = queue.shift();
temp.push(n.val);
if (n.left) queue.push(n.left);
if (n.right) queue.push(n.right);
}
ans.push(temp);
}
return ans;
};二叉树的层序遍历(Javascript语言完全版) (迭代 + 递归)
/**
* 102. 二叉树的层序遍历
* @param {TreeNode} root
* @return {number[][]}
*/
// 迭代
var levelOrder = function(root) {
const queue = [], res = [];
root && queue.push(root);
while(len = queue.length) {
const val = [];
while(len--) {
const node = queue.shift();
val.push(node.val);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
res.push(val);
}
return res;
};
// 递归
var levelOrder = function(root) {
const res = [];
function defs (root, i) {
if(!root) return;
if(!res[i]) res[i] = [];
res[i].push(root.val)
root.left && defs(root.left, i + 1);
root.right && defs(root.right, i + 1);
}
defs(root, 0);
return res;
};
/**
* 107. 二叉树的层序遍历 II
* @param {TreeNode} root
* @return {number[][]}
*/
// 迭代
var levelOrderBottom = function(root) {
const queue = [], res = [];
root && queue.push(root);
while(len = queue.length) {
const val = [];
while(len--) {
const node = queue.shift();
val.push(node.val);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
res.push(val);
}
return res.reverse()
};
// 递归
var levelOrderBottom = function(root) {
const res = [];
function defs (root, i) {
if(!root) return;
if(!res[i]) res[i] = [];
res[i].push(root.val);
root.left && defs(root.left, i + 1);
root.right && defs(root.right, i + 1);
}
defs(root, 0);
return res.reverse();
};
/**
* 199. 二叉树的右视图
* @param {TreeNode} root
* @return {number[]}
*/
// 迭代
var rightSideView = function(root) {
const res = [], queue = [];
root && queue.push(root);
while(l = queue.length) {
while (l--) {
const {val, left, right} = queue.shift();
!l && res.push(val);
left && queue.push(left);
right && queue.push(right);
}
}
return res;
};
// 递归
var rightSideView = function(root) {
const res = [];
function defs(root, i) {
if(!root) return;
res[i] = root.val;
root.left && defs(root.left, i + 1);
root.right && defs(root.right, i + 1);
}
defs(root, 0);
return res;
};
/**
* 637. 二叉树的层平均值
* @param {TreeNode} root
* @return {number[]}
*/
// 迭代
var averageOfLevels = function(root) {
const queue = [], res = [];
root && queue.push(root);
while(len = queue.length) {
let sum = 0, l = len;
while(l--) {
const {val, left, right} = queue.shift();
sum += val;
left && queue.push(left);
right && queue.push(right);
}
res.push(sum/len);
}
return res;
};
// 递归
var averageOfLevels = function(root) {
const resCount = [], res = [];
function defs(root, i) {
if(!root) return;
if(isNaN(res[i])) resCount[i] = res[i] = 0;
res[i] += root.val;
resCount[i]++;
root.left && defs(root.left, i + 1);
root.right && defs(root.right, i + 1);
}
defs(root, 0);
return res.map((val, i) => val / resCount[i]);
};
/**
* 515. 在每个树行中找最大值
* @param {TreeNode} root
* @return {number[]}
*/
// 迭代
const MIN_G = Number.MIN_SAFE_INTEGER;
var largestValues = function(root) {
const queue = [], res = [];
root && queue.push(root);
while(len = queue.length) {
let max = MIN_G;
while(len--) {
const {val, left, right} = queue.shift();
max = max > val ? max : val;
left && queue.push(left);
right && queue.push(right);
}
res.push(max);
}
return res;
};
// 递归
var largestValues = function(root) {
const res = [];
function defs (root, i) {
if(!root) return;
if(isNaN(res[i])) res[i] = root.val;
res[i] = res[i] > root.val ? res[i] : root.val;
root.left && defs(root.left, i + 1);
root.right && defs(root.right, i + 1);
}
defs(root, 0);
return res;
};
/**
* 429. N 叉树的层序遍历
* @param {Node|null} root
* @return {number[][]}
*/
// 迭代
var levelOrder = function(root) {
const queue = [], res = [];
root && queue.push(root);
while(len = queue.length) {
const vals = [];
while(len--) {
const {val, children} = queue.shift();
vals.push(val);
for(const e of children) {
queue.push(e);
}
}
res.push(vals);
}
return res;
};
// 递归
var levelOrder = function(root) {
const res = [];
function defs (root, i) {
if(!root) return;
if(!res[i]) res[i] = [];
res[i].push(root.val);
for(const e of root.children) {
defs(e, i + 1);
}
}
defs(root, 0);
return res;
};
/**
* 116. 填充每个节点的下一个右侧节点指针
* 117. 填充每个节点的下一个右侧节点指针 II
* @param {Node} root
* @return {Node}
*/
// 迭代
var connect = function(root) {
const queue = [];
root && queue.push(root);
while(len = queue.length) {
while(len--) {
const node1 = queue.shift(),
node2 = len ? queue[0] : null;
node1.next = node2;
node1.left && queue.push(node1.left);
node1.right && queue.push(node1.right);
}
}
return root;
};
// 递归
var connect = function(root) {
const res = [];
function defs (root, i) {
if(!root) return;
if(res[i]) res[i].next = root;
res[i] = root;
root.left && defs(root.left, i + 1);
root.right && defs(root.right, i + 1);
}
defs(root, 0);
return root;
};