KerrGeoPy is a python implementation of the KerrGeodesics Mathematica library. It is intended for use in computing orbital trajectories for extreme-mass-ratio inspirals (EMRIs). It implements the analytical solutions for plunging orbits from Dyson and van de Meent, as well as solutions for stable orbits from Fujita and Hikida. The library also provides a set of methods for computing constants of motion and orbital frequencies. See the documentation for more information.
Install using Anaconda
conda install -c conda-forge kerrgeopyor using pip
pip install kerrgeopyNote
This library uses functions introduced in scipy 1.8, so it may also be necessary to update scipy by running
pip install scipy -U, although in most cases this should be done automatically by pip. Certain plotting and animation functions also make use of features introduced in matplotlib 3.7 and rely on ffmpeg, which can be easily installed using homebrew or anaconda.
For contribution guidelines, see CONTRIBUTING.
KerrGeoPy computes orbits in Boyer-Lindquist coordinates
Note that
First, construct a StableOrbit using the four parameters described above.
import kerrgeopy as kg
from math import cos, pi
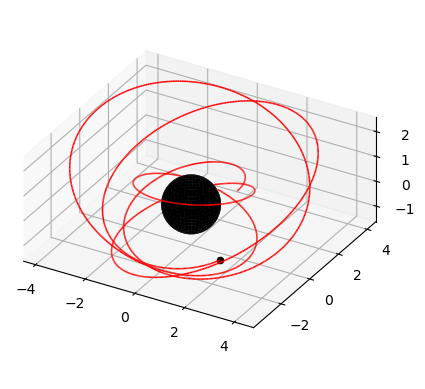
orbit = kg.StableOrbit(0.999,3,0.4,cos(pi/6))Plot the orbit from plot() method
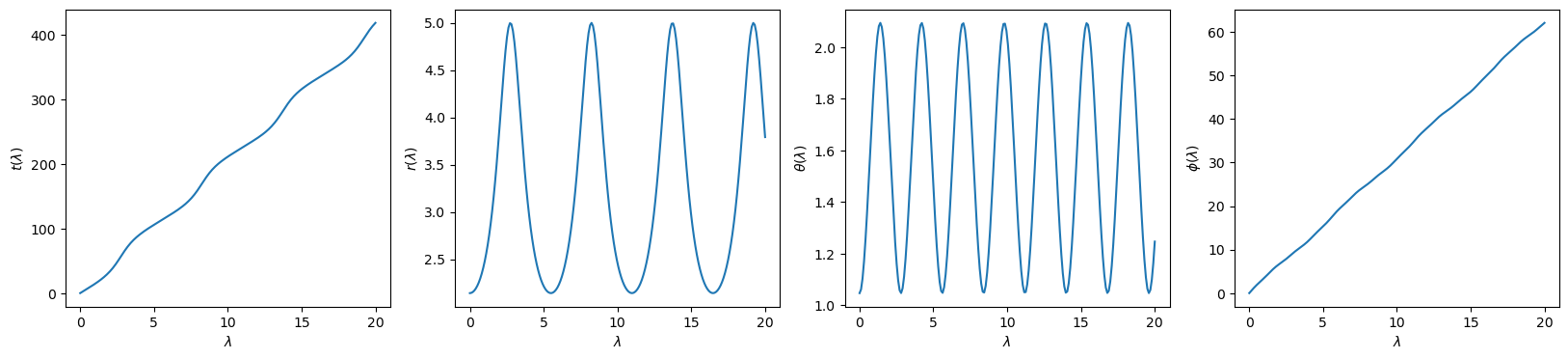
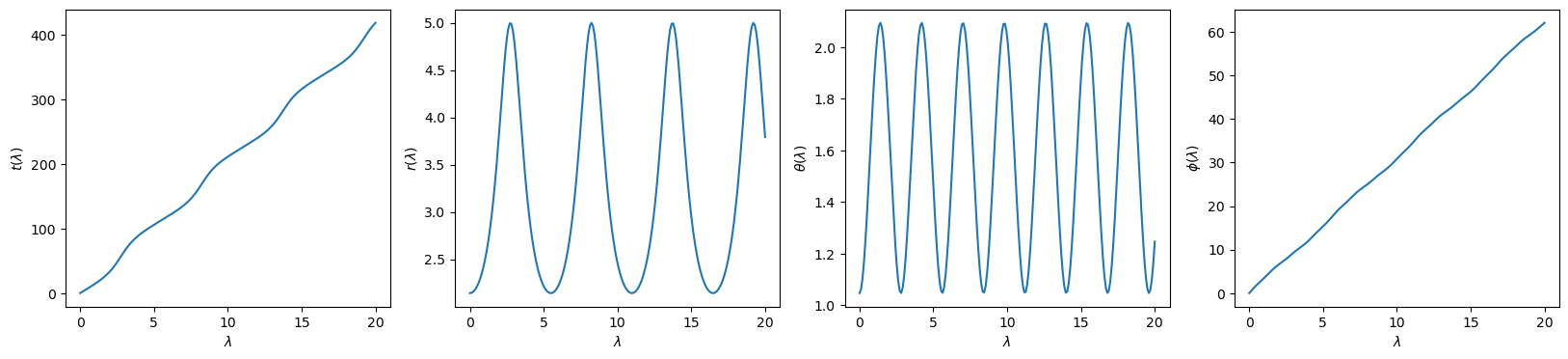
fig, ax = orbit.plot(0,10)Next, compute the time, radial, polar and azimuthal components of the trajectory as a function of Mino time using the trajectory() method. By default, the time and radial components of the trajectory are given in geometrized units and are normalized using
t, r, theta, phi = orbit.trajectory()import numpy as np
import matplotlib.pyplot as plt
time = np.linspace(0,20,200)
plt.figure(figsize=(20,4))
plt.subplot(1,4,1)
plt.plot(time, t(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$t(\lambda)$")
plt.subplot(1,4,2)
plt.plot(time, r(time))
plt.xlabel("$\lambda$")
plt.ylabel("$r(\lambda)$")
plt.subplot(1,4,3)
plt.plot(time, theta(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$\theta(\lambda)$")
plt.subplot(1,4,4)
plt.plot(time, phi(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$\phi(\lambda)$")Use the constants_of_motion() method to compute the dimensionless energy, angular momentum and Carter constant. By default, constants of motion are given in geometrized units where
Here,
Frequencies of motion can be computed in Mino time using the mino_frequencies() method and in Boyer-Lindquist time using the fundamental_frequencies() method. As with constants of motion, the frequencies returned by both methods are given in geometrized units and are normalized by
from IPython.display import display, Math
E, L, Q = orbit.constants_of_motion()
upsilon_r, upsilon_theta, upsilon_phi, gamma = orbit.mino_frequencies()
omega_r, omega_theta, omega_phi = orbit.fundamental_frequencies()
display(Math(fr"a = {orbit.a} \quad p = {orbit.p} \quad e = {orbit.e} \quad x = {orbit.x}"))
display(Math(fr"\mathcal{{E}} = {E:.3f} \quad \mathcal{{L}} = {L:.3f} \quad \mathcal{{Q}} = {Q:.3f}"))
display(Math(fr"""\Upsilon_r = {upsilon_r:.3f} \quad
\Upsilon_\theta = {upsilon_theta:.3f} \quad
\Upsilon_\phi = {upsilon_phi:.3f} \quad
\Gamma = {gamma:.3f}"""))
display(Math(fr"""\Omega_r = {omega_r:.3f} \quad
\Omega_\theta = {omega_theta:.3f} \quad
\Omega_\phi = {omega_phi:.3f}"""))Plunging orbits are parametrized using the spin parameter and the three constants of motion.
It is assumed that all orbital parameters are given in geometrized units where
Construct a PlungingOrbit by passing in these four parameters.
orbit = kg.PlungingOrbit(0.9, 0.94, 0.1, 12)As with stable orbits, the components of the trajectory can be computed using the trajectory() method
t, r, theta, phi = orbit.trajectory()import numpy as np
import matplotlib.pyplot as plt
time = np.linspace(0,20,200)
plt.figure(figsize=(20,4))
plt.subplot(1,4,1)
plt.plot(time, t(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$t(\lambda)$")
plt.subplot(1,4,2)
plt.plot(time, r(time))
plt.xlabel("$\lambda$")
plt.ylabel("$r(\lambda)$")
plt.subplot(1,4,3)
plt.plot(time, theta(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$\theta(\lambda)$")
plt.subplot(1,4,4)
plt.plot(time, phi(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$\phi(\lambda)$")Use the from_constants() class method to construct a StableOrbit from the spin parameter and constants of motion
orbit = kg.StableOrbit.from_constants(0.9, 0.95, 1.6, 8)Use the Orbit class to construct an orbit from the spin parameter
stable_orbit = kg.StableOrbit(0.999,3,0.4,cos(pi/6))
x0 = stable_orbit.initial_position
u0 = stable_orbit.initial_velocity
orbit = kg.Orbit(0.999,x0,u0)t, r, theta, phi = orbit.trajectory()
time = np.linspace(0,20,200)
plt.figure(figsize=(20,4))
plt.subplot(1,4,1)
plt.plot(time, t(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$t(\lambda)$")
plt.subplot(1,4,2)
plt.plot(time, r(time))
plt.xlabel("$\lambda$")
plt.ylabel("$r(\lambda)$")
plt.subplot(1,4,3)
plt.plot(time, theta(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$\theta(\lambda)$")
plt.subplot(1,4,4)
plt.plot(time, phi(time))
plt.xlabel("$\lambda$")
plt.ylabel(r"$\phi(\lambda)$")If you use this software, please cite our article in the Journal of Open Source Software.
@article{kerrgeopy,
doi = {10.21105/joss.06587},
url = {https://doi.org/10.21105/joss.06587},
year = {2024},
publisher = {The Open Journal},
volume = {9},
number = {98},
pages = {6587},
author = {Seyong Park and Zachary Nasipak},
title = {KerrGeoPy: A Python Package for Computing Timelike Geodesics in Kerr Spacetime},
journal = {Journal of Open Source Software}
}
- Seyong Park
- Zach Nasipak