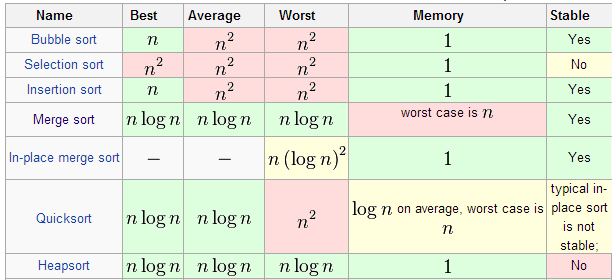- 涉及的概念
- 有序度,是有序元素对的数量,有序元素对满足,如果i<j,则a[i]<=a[j]
- 逆序度,是逆序对的数量,满足如果i<j,则a[i]>a[j]
- 满有序度,其中满有序度=有序度+逆序度
- 一般会从这几个方面比较不同的排序算法
- 最好,最坏,平均的时间复杂度情况
- 时间复杂度系数,常数,低阶
- 比较次数,交换次数
- 稳定性:稳定与否等介于相同大小值的顺序是否会被再次更改。
- 各排序复杂度情况
- 原理:每次遍历比较交换元素,找到最值,放到末尾。
- 比较或者交换的时候有序度加1,交换总次数是n*(n-1)/2-初始有序度,也就是逆序度。
- 稳定性:
- 稳定,因为大小相等不做交换。
- 复杂度
- 时间
- 最好情况,不需要交换,一次冒泡,时间复杂度O(n)
- 最坏情况,待排序输入正好是目标顺序的逆序,时间复杂度O(n^2)
- 最好情况,不需要交换,一次冒泡,时间复杂度O(n)
- 空间
- 平均情况下比较次数取中间值:n*(n-1)/4,取平均时间复杂度O(n^2)(非严格推导的复杂度)
- 空间复杂度上仅需要常量级的临时空间,是O(1),是原地排序算法。
- 时间
插入排序 java code
- 适用于少量元素的排序
- 有点冒泡升级版本的意味,也涉及到比较和移动元素。交换次数也是逆序度。
- 原理:分为两个区间,一个为排序区间,一个为未排序区间,初始状态下排序区间只有第一个元素,如果把第二个元素,也就是未排序区间的第一个元素,加入到排序区间中排序,然后继续拿未排序区间的第一个元素,加入排序区间去排序,直到完成排序。像扑克牌,抽牌插入手牌中排序。(注意,从算法实现上,从排序区间的尾部开始比较更佳,如果从首部开始,一次比较可能是n-1次移位,不是一个好方案,n是元素数量)
- 复杂度
- 空间 - 空间复杂度是O(1),是一个原地排序算法
- 时间 - 最好情况下,就是排好序的情况,每个数都比较一次即插入到本身位置,时间复杂度是O(n) - 最坏情况下,待排序输入正好是目标顺序的逆序,每次插入都在数组的首位插入,时间复杂度是O(n^2) - 平均情况下,O(n^2)
- 由于冒泡排序,虽然复杂度和交换次数一样;但是冒泡每次交换数据,都需要三次赋值操作,而插入排序仅需要一次赋值操作。
- 稳定性:
- 稳定,对于相同大小的值,先出现的排在前面。
选择排序 java code
- 原理:分为排序和未排序区间,每次都从未排序区间拿到最值,然后放到排序区间尾部(这个位置原来的数和最值位置交换,可能把与未排序区间数值大小相等的数字,放到更后面,所以不稳定)
- 空间复杂度O(1)
- 时间复杂度最坏最好平均都是O(n^2)
- 稳定性: - 不稳定,他的原理决定了它的不稳定性。
-
总是一分为二处理,处理好了再合并。分治思路+递归实现。
-
是一个稳定的算法,可以参看伪代码
-
时间复杂度是nlogn
- 稳定性:不稳定(和快排相比的重大缺点)
- 推导过程:
- T(n)=2*T(n/2)+n 每次合并都需要两个子数据的时间和合并两个子数组的时间
- T(n)=2*(2T(n/4)+n/2)+n=4T(n/4)+2n ..
- T(n)=2^mT(n/(2^m))+m*n
- 当T(n/(2^m))=T(1)时 -->n/(2^m)=1-->m=log2 (n)-->T(n)=C*n+log2(n)*n (注:C是一个常数)-->O(nlogn)
- 非原地排序算法(合并子数组,需要额外空间)
- 空间复杂度是O(n)(临时存储空间n)
- T(n)=2*T(n/2)+n 每次合并都需要两个子数据的时间和合并两个子数组的时间
-
大体思路如下,具体可以看代码实现 java code
mergesort(int[] array,int n){
//n=array.lenth
merge(array,0,n-1);
}
merge(int[] array,int start,int end){
if(start>end){
return;
}
int middle=(start+end)/2;
merge(array,start,middle);
merge(array,middle+1,end);
mergeArray(array[start..end],array[start..middle],array[middle+1..end])
}
mergeArray(array[start..end],array[start..middle],array[middle+1..end]){
int i=start,j=midlle+1,k=0;
int[] temp=new int[]{end-start};
while(i<=midlle&&j<=end){
if(array[i]<=array[j]){
temp[k++]=array[i++];
}else{
temp[k++]=array[j++];
}
}
int tempStart,tempEnd;
//Judging who do not finish task.
if(i<=middle){
tempStart=i;
tempEnd=middle;
}else{
tempStart=j;
tempEnd=end;
}
//do work remaining
while(tempStart<=tempEnd){
temp[k++]=array[tempStart];
}
//copy temp to array
for(int index=0;index<array.length;i++){
array[index]=temp[index];
}
}
或者你可以借助哨兵模式来简化判断条件- 思路从数组中是找到一个元素作为分区点,小于它的排在左边,大于它的排在右边;然后在左右区间继续找分区点,重复上一次操作,直到排序完成。分治思想+递归实现。锚点可以选定数组的最后一个元素(或者区间内随机的任意一个元素)。但是一个区间,排序完成后,锚点会位于区间的中间位置。
- 原地排序算法,这优于归并排序。
- 时间复杂度是O(nlogn),和归并一样
- 推导过程:
- T(n)=2*T(n/2)+n 每次分区都需要两个子数据的时间加上找到分区点的时间
- T(n)=2*(2T(n/4)+n/2)+n=4T(n/4)+2n ..
- T(n)=2^mT(n/(2^m))+m*n
- 特殊值法,当T(n/(2^m))=T(1)时 -->n/(2^m)=1
- 所以m=log2 (n)-->T(n)=C*n+log2(n)*n (注:C是一个常数) -->O(nlogn)
- 推导过程:
- 不稳定,分区点在交换的时候就可能导致不稳定
- 极端情况下是O(n^2),比如递增数组,每次又选最后一个数为分区点。
- java code
//伪代码如下
quicksort(array){
sort(array,0,arry.length-1)
}
sort(array,start,end){
if(start>=end){
return
}
//获取分区点下标
indexP=getPartition(array,start,end)
sort(array,start,indexP-1)
sort(array,indexP+1,end)
}
getPartition(array,start,end){
p=array[end]
i,j=start
while(j<end){
if(array[j]<=p){
swap array[i] with array[j]
i++
//i左边的数都小于p
}else{
//延迟交换
}
j++
}
swap array[i] with array[end]
return i;
}- 层级
- 终止条件
- 剪掉非最优的无用分支,优化复杂度,像给树修剪枝干。
- 专注最优解,把非最优解的分支剪除。
- 类似一层层的水波;算法实现上思路上很像摇色子,一层层向外把每层色子扫进色子杯中,在扫下一层前,先把色子一一拿出(扫一下层的动作等介于拿出色子的时候把下一层的子色子放进杯中)
- 复杂度
- 偏向暴力求解
- leetcoe:104,111
- 伪代码
BFS(Node){
queue=LinkedList<>();
queue.add(Node);
while(!queue.isEmpty){
node=queue.poll();
...
Nodes=getRelativeNodes(node);
queue.add(Nodes);
...
}
}- 回溯思想
- 类似走迷宫,适合递归实现或者迭代实现
- 复杂度
- 偏向暴力求解
- leetcoe:104,111
- 条件
- 有序数据,可以通过下标找到数据,可以理解为仅使用于数组
- 数据相对而言是静态的,不会频繁变化
- 数据量小且比较操作不耗时也没必要用二分查找
- 数据大也用不了,因为数组要求连续的内存空间,如果内存吃紧也不适合
- 时间复杂度O(logn)
- 具体实现:java code
- 递归法伪代码:
binarySearch(int[] array,int target){
search(array,target,0,array.length-1);
}
search(int[] array,int target,int start,int end){
int middle=start+(end-start)>>1;
if(target==array[middle]){
return middle;
}else if(target>array[middle]){
return search(array,target,middle+1,end);
}else{
return search(array,target,start,middle-1);
}
}- 遍历法伪代码:
binarySearch(int[] array,int target){
search(array,target,0,array.length-1);
}
search(int[] array,int target,int start,int end){
while(start<=end){
int mid=start+((end-start)>>1)
if(array[mid]==target){
return mid;
}else if(target>array[mid]){
start=mid+1;
}else{
end=mid-1;
}
}
return -1;
}- Divide:Problem-->SubProblem1,SubProblem2...
- Conquer:SubProblem1-->Answer1,SubProbelm2-->Answer2.....
- Merge:Answer1+Answer2+...=Answer
- 条件
- 可以分治
- 每次都决定一个当前最优选项
- 缺点:解决的问题范围小,不可修改做过的决定
- 条件
- 可以分治
- 存储每一步的决定,可回退
- 堆必须是一个完全二叉树。完全二叉树要求,除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。
- 堆中的每个节点的值必须大于等于(或者小于等于)其子树中每个节点的值
- PriorityQueue(默认是递增的队列,也就是小顶堆),求最值(或者第几大元素),求中位数等场景 (leetcode 703.)
- 实现机制可以是HEAP
- 也可以是 BinarySeachTree
Queue<Integer> q = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
//System.out.println("o1=" + o1 + ",o2=" + o2);
//o2 is in front of o1
//if (o1>o2){
//return 1;//正数递增
//}else {
//return -1;//负数递减
//}
return o2 - o1;
}
});
- 非线性表结构
- 元素
- 定点
- 边
- 度
- 权重
- 实现
- 领接矩阵
- 领接表
- LRU
- 新增数据被添加到链表头部,添加满了,最后的数据是被丢弃。Lru
- 真正支配世界的十种算法
- 刷 LeetCode 吃力正常吗?
- 水中的鱼 blog
- 数据结构与算法 知乎专栏
- The 10 must-know algorithms and data structures for a software engineer
- 数据结构与算法之美
- CS-Notes
- s32n/algorithm
- 坐在马桶上学算法