Miniaturizing transistors, the building blocks of integrated circuits, presents significant challenges for the semiconductor industry. Precisely measuring these features during production is crucial for high-quality chips. Existing in-line metrology techniques, such as optical critical-dimension (OCD) scatterometry and critical-dimension scanning electron microscopy (CD-SEM), are nearing their limits. OCD struggles with the inherent limitations of light and shrinking features, while CD-SEM, despite providing valuable insights, is restricted by sampling area and resolution. To overcome these obstacles, the industry is exploring X-ray-based metrology. X-rays, with their shorter wavelengths, allow for more precise analysis and are sensitive to variations in composition, providing richer data.
CD-SAXS (Critical Dimension Small Angle X-ray Scattering) is a promising technique for nano-structure electronics. It uses a transmission geometry, sending the beam through the sample and the 750 micrometer-thick silicon wafer. The x-ray spot size varies between 10-1000 μm, enabling the measurement of small patterned areas. Studies have shown CD-SAXS's effectiveness in characterizing the shape and spacing of nanometer-sized patterns.
Although several big companies are developing software for CD-SAXS, this technique is still in its infancy and there isn't an open source coherent package available for its data analysis. Thus, this cdsaxs package is aimed at providing simulation and fitting tools for CD-SAXS synchotron data for researchers.
The collection of functions developed at CEA (French Alternative Energies and Atomic Energy Commission) by former PhD students and at Lawrence Berkeley National Laboratory and Brookhaven National Laboratory served as the foundation for this package.
To install cdsaxs, it is recommended to use a virtual environment. Follow these steps:
-
Create a virtual environment named
cdsaxs-venv:python -m venv cdsaxs-venv
-
Activate the virtual environment:
- On Windows:
cdsaxs-venv\Scripts\activate
- On macOS and Linux:
source cdsaxs-venv/bin/activate
- On Windows:
-
Install
cdsaxsfrom PyPI:pip install cdsaxs
-
Alternatively, install the latest version from the GitHub repository:
pip install git+https://github.com/CEA-MetroCarac/cdsaxs.git
-
Or clone the repository and install the package:
git clone https://github.com/CEA-MetroCarac/cdsaxs.git cd cdsaxs pip install .
Two models were considered in the development of this code. The first model focuses on the cross section of a line in a line-space pattern. In this model, the cross section of a line is represented by a stack of trapezoids, which collectively form the shape of the cross section. This model is known as the Stacked Trapezoid Model.
 |
|---|
| SEM image in a) is a cross-section of a line in SEM image in b). The black trapezoidal shapes in a) represent the modelling done for this simulation. |
The second model introduces another concept known as the Strong Castle Model. This model builds upon the previous one by incorporating an additional nano-structure on top, resulting in an overlay. It provides a tool for representing the overlay between multiple structures.
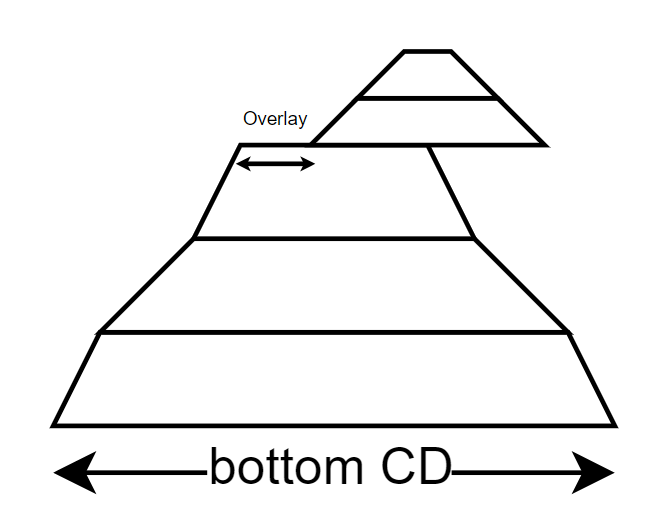 |
|---|
| Strong castle model where top structure is not aligned thus we have an overlay. |
To calculate the intensity profile of the scattering pattern, we perform a Fourier transformation on each trapezoid and then add them. The Fourier transformation of a trapezoid can be expressed using the following equation:
where,
The intensity map obtained from synchotron experiment looks like following:
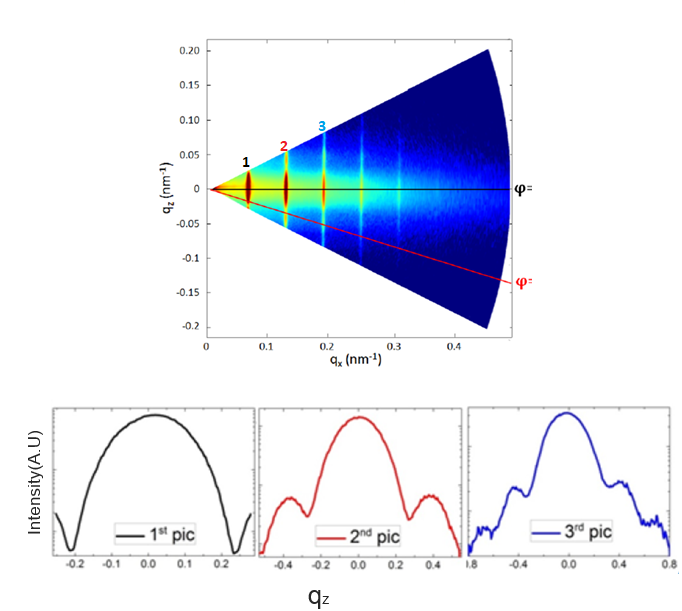 |
|---|
| Intensity map and vertical cut of corresponding bragg order |
Vertical cut along the different bragg order is made to get the intensity profile shown below the intensity map. These profiles are the experimental data that we want to fit.
The objective of the fitting is to iterate over a high number of different line profile (represented as various combination of stacked trapezoids) and to converge towards the profile that its Fourier Transform will best match the experimental data. While the objective seems simple to describe, the problem is complex. Traditional optimization methods used for refinement often fall short when dealing with complex internal structures with numerous parameters, either being trapped in local minima or not converging toward the same solutions.
Another challenge arises from the possibility of "degenerate" solutions. These occur when multiple structural models can produce the same scattering data, making it difficult to pinpoint the true structure. This is a common issue in scattering analysis.
Therefore, the ideal scenario for CD-SAXS analysis involves an optimization algorithm that can consistently and rapidly converge on the best possible fit for the data. While some prior knowledge about the underlying structure can accelerate the process, such information is not always readily available. This highlights the need for more efficient algorithms that can handle complex structures even with limited prior knowledge.
Genetic and evolutionary algorithms have emerged as promising alternatives. These methods mimic biological evolution, with the model parameters acting as the "genetic code." Starting with randomly generated parameters, these algorithms iteratively refine them through a "mixing strategy" over multiple generations until the optimal set is found. This approach excels at searching large parameter spaces with wide bounds, making it suitable for our purposes.
One algorithm is the Covariance Matrix Adaptation Evolution Strategy (CMAES). This method is particularly well-suited for high-dimensional optimization problems, making it ideal for complex nano-structure analysis. CMAES operates by maintaining a population of candidate solutions, with each iteration generating new candidates based on the previous generation performance. By adapting the covariance matrix of the candidate solutions, CMAES can efficiently explore the parameter space and converge on the optimal solution. The implementation of deap library is used for this purpose.
For CD-SAXS experiment, the algorithm starts with the experimental data collected. Then, a series of in-depth line profile generated, through a set of parameters as describe earlier. Afterwards, the calculated analytical Fourier transform is compared with the experimental data using a mean-absolute error log:
where
We repeat this process until we are satisfied with the precision of the fit. The final set of parameters that gives the best fit and it's fitness value which is the output of the algorithm.
The CMAES algorithm provides a single best-fit solution for the nano-structure parameters. However, it is essential to understand the uncertainty associated with these parameters. This uncertainty relates to the different possible combinations of parameters that could result in a similar goodness of fit. For instance, decreasing slightly height of one trapezoid and increasing the height of another can result in a similar goodness of fit. To address this, we can use MCMC algorithm to explore and find all the sets of population that can result in the same goodness of fit. The emcee library was very handy for this purpose.
Once all the population of possible solutions are found we can use it to obtain the statistical information about the parameters. Notably the uncertainty of the parameters using the confidence interval.
Please consult the tutorials folder for more information on how to use the package.
Please refer to the CONTRIBUTING.md file for more information on how to contribute to the project.


