Strip outputs from .ipynb files [skip ci]

AC1/r-proxy-controls.Rmd

@@ -0,0 +1,200 @@
+---
+title: An R Markdown document converted from "AC1/r-proxy-controls.irnb"
+output: html_document
+---
+
+# Negative (Proxy) Controls for Unobserved Confounding
+
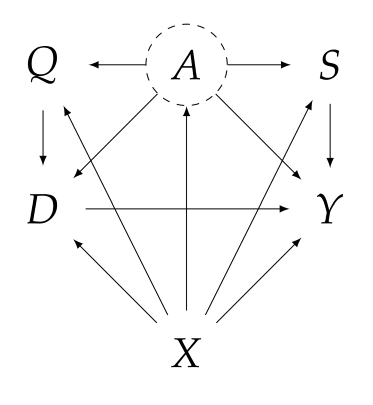
+Consider the following SEM, where $Y$ is the outcome, $D$ is the treatment, $A$ is some unobserved confounding, and $Q$, $X$, $S$ are the observed covariates. In particular, $Q$ is considered to be the proxy control treatment as it a priori has no effect on the actual outcome $Y$, and $S$ is considered to be the proxy control outcome as it a priori is not affected by the actual treatment $D$. See also [An Introduction to Proximal Causal Learning](https://arxiv.org/pdf/2009.10982.pdf), for more information on this setting.
+
+![proxy_dag.png](https://raw.githubusercontent.com/stanford-msande228/winter23/main/proxy_dag.png)
+
+Under linearity assumptions, the average treatment effect can be estimated by solving the vector of moment equations:
+\begin{align}
+E\left[(\tilde{Y} - \alpha \tilde{D} - \delta \tilde{S}) \left(\begin{aligned}\tilde{D}\\ \tilde{Q}\end{aligned}\right) \right] = 0
+\end{align}
+where for every variable $V$ we denote with $\tilde{V} = V - E[V|X]$.
+
+When the dimension of the proxy treatment variables $Q$ is larger than the dimension of proxy outcome variables $S$, then the above system of equations is over-identified. In these settings, we first project the "technical instrument" variables $\tilde{V}=(\tilde{D}, \tilde{Q})$ onto the space of "technical treatment" variables $\tilde{W}=(\tilde{D}, \tilde{S})$ and use the projected $\tilde{V}$ as a new "technical instrument". In particular, we run an OLS regression of $\tilde{W}$ on $\tilde{V},$ and define $\tilde{Z} = E[\tilde{W}\mid \tilde{V}] = B \tilde{V}$, where the $t$-th row $\beta_t$ of the matrix $B$ is the OLS coefficient in the regression of $\tilde{W}_t$ on $\tilde{V}$. These new variables $\tilde{Z}$, can also be viewed as engineered technical instrumental variables. Then we have the exactly identified system of equations:
+\begin{align}
+E\left[(\tilde{Y} - \alpha \tilde{D} - \delta \tilde{S}) \tilde{Z} \right] := E\left[(\tilde{Y} - \alpha \tilde{D} - \delta \tilde{S}) B \left(\begin{aligned}\tilde{D}\\ \tilde{Q}\end{aligned}\right) \right] = 0
+\end{align}
+
+The solution to this system of equations is numerically equivalent to the following two stage algorithm:
+- Run OLS of $\tilde{W}=(\tilde{D}, \tilde{S})$ on $\tilde{V}=(\tilde{D}, \tilde{Q})$
+- Define $\tilde{Z}$ as the predictions of the OLS model
+- Run OLS of $\tilde{Y}$ on $\tilde{Z}$.
+This is the well-known Two-Stage-Least-Squares (2SLS) algorithm for instrumental variable regression.
+
+Since we're considering only linear models and in a low-dimensional setting, we'll focus on just using linear IV methods.
+
+```{r}
+install.packages("hdm")
+```
+
+```{r}
+library(hdm)
+
+set.seed(1)
+```
+
+# Analyzing Simulated Data
+
+First, let's evaluate the methods on simulated data generated from a linear SEM characterized by the above DAG. For this simulation, we'll set the ATE to 2.
+
+```{r}
+gen_data <- function(n, ate) {
+  X <- matrix(rnorm(n * 10), ncol = 10)
+  A <- 2 * X[, 1] + rnorm(n)
+  Q <- 10 * A + 2 * X[, 1] + rnorm(n)
+  S <- 5 * A + X[, 1] + rnorm(n)
+  D <- Q - A + 2 * X[, 1] + rnorm(n)
+  Y <- ate * D + 5 * A + 2 * S + 0.5 * X[, 1] + rnorm(n)
+  return(list(X, A, Q, S, D, Y))
+}
+```
+
+```{r}
+data_list <- gen_data(5000, 2)
+X <- data_list[[1]]
+A <- data_list[[2]]
+Q <- data_list[[3]]
+S <- data_list[[4]]
+D <- data_list[[5]]
+Y <- data_list[[6]]
+```
+
+We define the technical instrument $V=(D, Q)$ and technical treatment $W=(D, S)$. Estimating the treatement effect is then just a matter of solving an instrument variable regression problem with instruments $V$ and treatments $W$ and looking at the first coefficient associated with $D$.
+
+```{r}
+W <- cbind(D, S)
+V <- cbind(D, Q)
+```
+
+```{r}
+piv <- tsls(X, W, Y, V, homoscedastic = FALSE)
+cat("Estimated coefficient:", piv$coefficients["D", 1], "\n")
+cat("Standard error:", piv$se["D"], "\n")
+```
+
+# With Cross-Fitting
+
+We can also consider partialling out the controls using DML with cross-fitting
+
+```{r}
+lm_dml_for_proxyiv <- function(x, d, q, s, y, dreg, qreg, yreg, sreg, nfold = 5) {
+  # this implements DML for a partially linear IV model
+  nobs <- nrow(x)
+  foldid <- rep.int(1:nfold, times = ceiling(nobs / nfold))[sample.int(nobs)]
+  I <- split(1:nobs, foldid)
+  # create residualized objects to fill
+  ytil <- dtil <- qtil <- stil <- rep(NA, nobs)
+  # obtain cross-fitted residuals
+  cat("fold: ")
+  for (b in seq_along(I)) {
+    dfit <- dreg(x[-I[[b]], ], d[-I[[b]]]) # take a fold out
+    qfit <- qreg(x[-I[[b]], ], q[-I[[b]]]) # take a fold out
+    yfit <- yreg(x[-I[[b]], ], y[-I[[b]]]) # take a fold out
+    sfit <- sreg(x[-I[[b]], ], s[-I[[b]]]) # take a fold out
+    dtil[I[[b]]] <- (d[I[[b]]] - x[I[[b]], ] %*% as.matrix(dfit$coefficients)) # record residual
+    qtil[I[[b]]] <- (q[I[[b]]] - x[I[[b]], ] %*% as.matrix(qfit$coefficients)) # record residual
+    ytil[I[[b]]] <- (y[I[[b]]] - x[I[[b]], ] %*% as.matrix(yfit$coefficients)) # record residial
+    stil[I[[b]]] <- (s[I[[b]]] - x[I[[b]], ] %*% as.matrix(sfit$coefficients)) # record residual
+    cat(b, " ")
+  }
+  ivfit <- tsls(y = ytil, d = cbind(dtil, stil), x = NULL, z = cbind(dtil, qtil),
+                intercept = FALSE, homoscedastic = FALSE)
+  coef_est <- ivfit$coef[1] # extract coefficient
+  se <- ivfit$se[1] # record standard error
+  cat(sprintf("\ncoef (se) = %g (%g)\n", coef_est, se))
+  return(list(coef_est = coef_est, se = se, dtil = dtil, qtil = qtil,
+              ytil = ytil, stil = stil, foldid = foldid, spI = I))
+}
+```
+
+We'll just use OLS for partialling out again. We could of course try something more elaborate if we wanted.
+
+```{r}
+dreg <- function(x, d) {
+  lm.fit(x, d)
+} # ML method=ols
+qreg <- function(x, q) {
+  lm.fit(x, q)
+} # ML method=ols
+yreg <- function(x, y) {
+  lm.fit(x, y)
+} # ML method=ols
+sreg <- function(x, s) {
+  lm.fit(x, s)
+} # ML method=ols
+
+dml_piv <- lm_dml_for_proxyiv(X, D, Q, S, Y, dreg, qreg, yreg, sreg, nfold = 5)
+dml_piv
+```
+
+## Real Data - Effects of Smoking on Birth Weight
+
+In this study, we will be studying the effects of smoking on baby weight. We will consider the following stylized setup:
+
+Outcome ($Y$): baby weight
+
+Treatment ($D$): smoking
+
+Unobserved confounding ($A$): family income
+
+The observed covariates are put in to 3 groups:
+
+
+*   Proxy treatment control ($Q$): mother's education
+*   Proxy outcome control ($S$): parity (total number of previous pregnancies)
+*   Other observed covariates ($X$): mother's race and age
+
+
+Education serves as a proxy treatment control $Q$ because it reflects unobserved confounding due to household income $A$ but has no direct medical effect on birth weight $Y$. Parity serves as a proxy outcome control $S$ because family size reflects household income $A$ but is not directly caused by smoking $D$ or education $Q$.
+
+A description of the data used can be found [here](https://www.stat.berkeley.edu/users/statlabs/data/babies.readme).
+
+```{r}
+data <- read.table("https://www.stat.berkeley.edu/users/statlabs/data/babies23.data", header = TRUE)
+summary(data)
+```
+
+```{r}
+# Filter data to exclude entries where income, number of cigarettes smoked,
+# race, age are not asked or not known
+data <- data[data$race != 99, ]
+data <- data[!(data$number %in% c(98, 99)), ]
+data <- data[!(data$inc %in% c(98, 99)), ]
+data <- data[data$age != 99, ]
+dim(data)
+```
+
+```{r}
+# Create matrices for X, D, Q, S, A, Y
+X <- model.matrix(~ 0 + C(race) + age, data)
+D <- model.matrix(~ 0 + number, data)
+Q <- model.matrix(~ 0 + ed, data)
+S <- model.matrix(~ 0 + parity, data)
+A <- model.matrix(~ 0 + inc, data)
+Y <- model.matrix(~ 0 + wt, data)
+```
+
+```{r}
+# Use cross-fitting with OLS to estimate treatment effect within linear model context
+dreg <- function(x, d) {
+  lm.fit(x, d)
+} # ML method=ols
+qreg <- function(x, q) {
+  lm.fit(x, q)
+} # ML method=ols
+yreg <- function(x, y) {
+  lm.fit(x, y)
+} # ML method=ols
+sreg <- function(x, s) {
+  lm.fit(x, s)
+} # ML method=ols
+
+dml_bw_piv <- lm_dml_for_proxyiv(X, D, Q, S, Y, dreg, qreg, yreg, sreg, nfold = 5)
+dml_bw_piv
+```
+