AABB.cc

Copyright © 2016-2018 Lester Hedges

Released under the Zlib license.

About

A C++ implementation of a dynamic bounding volume hierarchy (BVH) using axis-aligned bounding boxes (AABBs). The data structure provides an efficient way of detecting potential overlap between objects of arbitrary shape and size and is commonly used in computer game engines for collision detection and ray tracing.

Because of their speed and flexibility, AABB trees are also well suited to overlap detection in physics applications, such as molecular simulation. They are particularly helpful for systems where there is a large size disparity between particle species, or whenever the particle density is extremely inhomogeneous. In such situations, traditional neighbour finding tools, such as cell lists, can become extremely inefficient (both in terms of memory footprint, and search speed). A good overview of the pros and cons of various neighbour finding algorithms can be found here. (Note that this only discusses the cost of querying different data structures, not the additional overhead of building them, or maintaining them as objects move around.)

In statistical physics, a common means of approximating a bulk (infinite) system is through the use of periodic boundary conditions. Here, particles that are on opposite sides of the unit box can interact through its periodic image. This library supports periodic and non-periodic systems in two and three dimensions. Support is also provided for simulation boxes that are partially periodic, i.e. periodic along specific axes. At present, only orthorhombic simulation boxes are supported.

The code in this library was adapted from parts of the Box2D physics engine.

Installation

A Makefile is included for building and installing the AABB library.

To compile and install the library, documentation, python wrapper, and demos:

make build
make install

By default, the library installs to /usr/local. Therefore, you may need admin privileges for the final make install step above. An alternative is to change the install location:

make PREFIX=MY_INSTALL_DIR install

If you would rather use a header-only version of the library in your application, simply run:

make header-only

The resulting library header, header-only/AABB.hpp, can be directly included in your source code without the need for compiling and linking.

Further details on using the Makefile can be found by running make without a target, i.e.

make

Compiling and linking

To use the library with a C/C++ code first include the library header file in the code.

#include <aabb/AABB.h>

Then to compile, we can use something like the following:

g++ example.cc -laabb

This assumes that we have used the default install location /usr/local. If we specify an install location, we would use a command more like the following:

g++ example.cc -I/my/path/include -L/my/path/lib -laabb

Python wrapper

A python wrapper can be built using:

make python

You will require python2.7 (and the development files if your package manager separates them) and SWIG. To use the module you will need the python file aabb.py and the shared object _aabb.so from the python directory. If you wish to use a different version of python, simply override the PYTHON make variable on the command line, e.g.

make PYTHON=3.5 python

(Note that you'll also need to update the shebang at the top of hard_disc.py to reflect your changes in order for the python demo to work.)

Example

Let's consider a two-component system of hard discs in two dimensions, where one species is much larger than the other. Making use of AABB trees, we can efficiently search for potential overlaps between discs by decomposing the system into its two constituent species and constructing a tree for each one. To test overlaps for any given disc, we simply query the two trees independently in order to find candidates. This decomposition ensures that each AABB tree has a well defined length scale, making it simple to construct and quick to query.

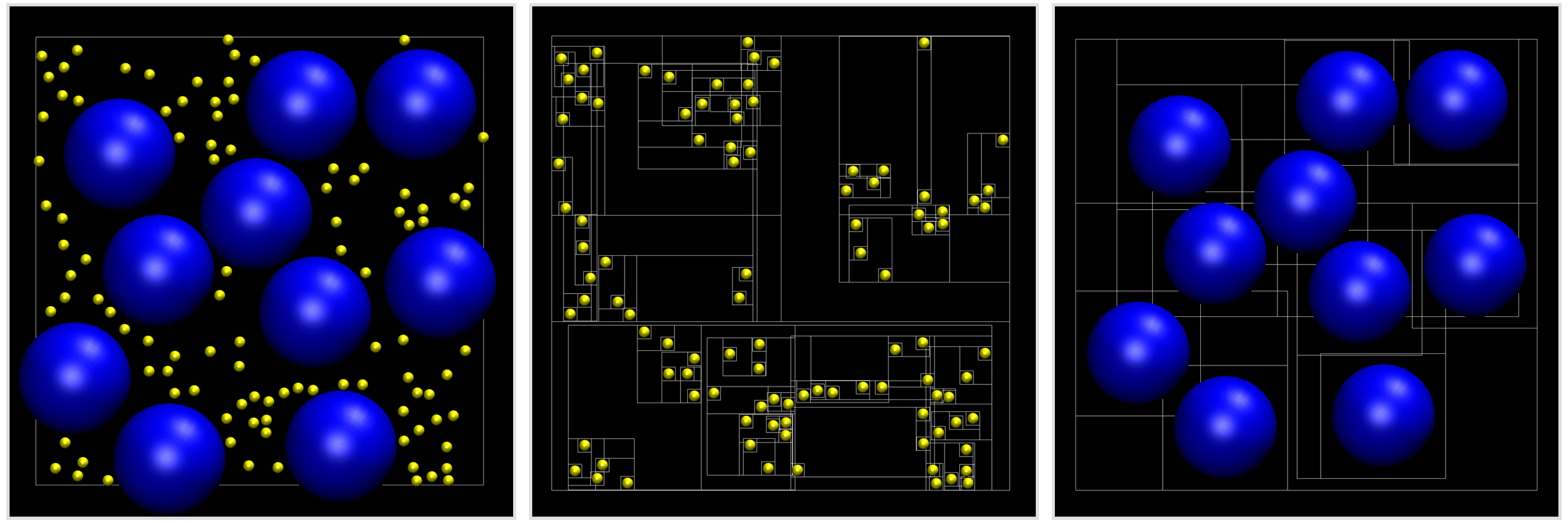
The image below shows the example hard disc system (left) and the AABB tree structures for each species (middle and right). Each leaf node in a tree is the AABB of an individual disc. Moving up the tree, AABBs are grouped together into larger bounding volumes in a recursive fashion, leading to a single AABB enclosing all of the discs at the root. The box outline in the left-hand image shows the periodic boundary of the system.

To query overlaps between discs we start at the root node and traverse the tree. At each node we test whether the current AABB overlaps the AABB of the chosen disc. If so, we add the two children of the node to the stack of nodes to test. Whenever we reach a leaf node with which an overlap is found we record a potential overlap with that disc (we know that the AABBs of the discs overlap, but we need still need to check that discs themselves actually overlap). The animation below shows an example of such a query. The disc of interest is highlighted in green and the boundary of the periodic simulation box is shown in orange. At each stage of the search the AABB of the current node in the tree is shown in white. Leaf nodes that overlap with the trial disc are highlighted green. Note that the green leaf node on the right-hand edge of the simulation box overlaps through the periodic boundary.

You may be wondering why the AABBs shown in the previous animation are not the minimum enclosing bounding box for each disc. This is a trick that is used to avoid frequent updates of the AABB tree during dynamics (movement of the discs). Whenever an AABB changes position we need to delete it from the tree then reinsert the new one (at the updated position). This can be a costly operation. By "fattening" the AABBs a small amount it is possible to make many displacements of the objects before an update is triggered, i.e. when one of the discs moves outside of its fattened AABB. During dynamics it is also possible for the tree to become unbalanced, leading to increasingly inefficient queries. Here trees are balanced using a surface area heuristic and active balancing is handled via tree rotations. The animation below shows an example of a hard disc simulation. Dynamic AABB trees were used to maintain a configuration of non-overlapping discs throughout the trajectory.

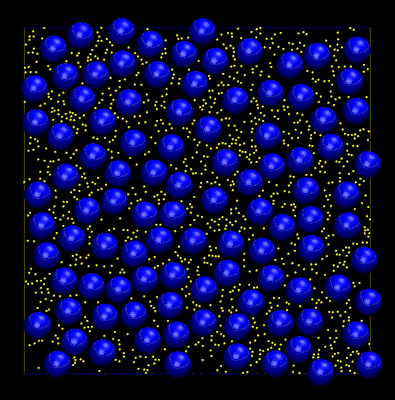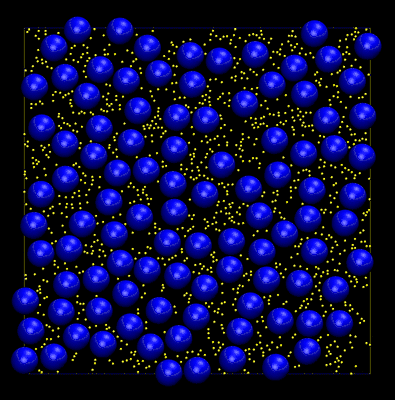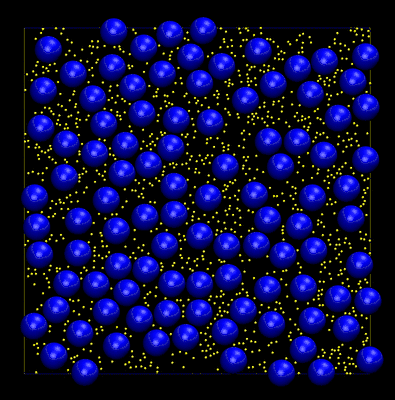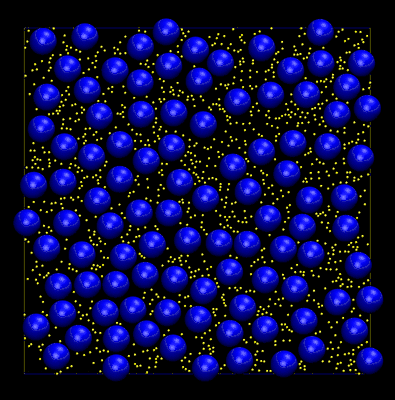
The code used to create the above animation can be found at demos/hard_disc.cc. When the library is built, you can run the demo and use VMD to view the trajectory as follows:

./demos/hard_disc
vmd trajectory.xyz -e demos/vmd.tcl

A python version of the demo can be found at python/hard_disc.py. This provides an example of how to use the python wrapper module.

Usage

There are several steps that go into building and using an AABB tree. Below are some examples showing how to use the various objects within the library.

AABB

This should be the minimum enclosing axis-aligned bounding box for an object in your simulation box. There is no need to fatten the AABB; this will be done when an object is inserted into the AABB tree. For example, to create an AABB for a two-dimensional disc we could do the following:

// Particle radius.
double radius = 1.0;

// Set the particle position.
std::vector<double> position({10, 10});

// Compute lower and upper AABB bounds.
std::vector<double> lowerBound({position[0] - radius, position[1] - radius});
std::vector<double> upperBound({position[0] + radius, position[1] + radius});

// Create the AABB.
aabb::AABB aabb(lowerBound, upperBound);

(While we refer to particles in this example, in practice a particle could be any object, e.g. a sprite in a computer game.)

Tree

Initialising a tree

To instantiate dynamic AABB trees for a periodic two-component system in two dimensions:

// Fattening factor.
double fatten = 0.1;

// Periodicity of the simulation box.
std::vector<bool> periodicity({true, true});

// Size of the simulation box.
std::vector<double> boxSize({100, 100});

// Number of small discs.
unsigned int nSmall = 100;

// Number of large discs.
unsigned int nLarge = 10;

// Create the AABB trees.
aabb::Tree treeSmall(2, fatten, periodicity, boxSize, nSmall);
aabb::Tree treeLarge(2, fatten, periodicity, boxSize, nLarge);

Many of the arguments to the constructor of Tree are optional, see the Doxygen documentation for details.

Note that both the periodicity and box size can be changed on-the-fly, e.g. for changing the box volume during a constant pressure simulation. See the setPeriodicity and setBoxSize methods for details.

Inserting a particle

To insert a particle (object) into the tree:

// Particle radius.
double radius = 1.0;

// Particle index (key).
unsigned int index = 1;

// Set the particle position.
std::vector<double> position({10.0, 10.0});

// Compute lower and upper AABB bounds.
std::vector<double> lowerBound({position[0] - radius, position[1] - radius});
std::vector<double> upperBound({position[0] + radius, position[1] + radius});

// Insert particle into the tree.
tree.insertParticle(index, position, lowerBound, upperBound);

Here index is a key that is used to create a map between particles and nodes in the AABB tree. The key should be unique to the particle and can take any value between 0 and std::numeric_limits<unsigned int>::max() - 1.

For spherical objects, the insertion can be simplified to:

tree.insertParticle(index, position, radius);

Removing a particle

If you are performing simulations using the grand canonical ensemble you may wish to remove particles from the tree. To do so:

tree.removeParticle(index);

where index is the key for the particle to be removed. (You'll need to keep track of the keys).

Querying the tree

You can query the tree for overlaps with a specific particle, or for overlaps with an arbitrary AABB object. The query method returns a vector containing the indices of the AABBs that overlap. You'll then need to test the objects enclosed by these AABBs for actual overlap with the particle of interest. (using your own overlap code).

For a particle already in the tree:

// Query AABB overlaps for particle with key 10.
std::vector<unsigned int> particles = tree.query(10);

For an arbitrary AABB:

// Set the AABB bounds.
std::vector<double> lowerBound({5, 5}};
std::vector<double> upperBound({10, 10}};

// Create the AABB.
aabb::AABB aabb(lowerBound, upperBound);

// Query the tree for overlap with the AABB.
std::vector<unsigned int> particles = tree.query(aabb);

Tests

The AABB tree is self-testing if the library is compiled in development mode, i.e.

make devel

Disclaimer

Please be aware that this a working repository so the code should be used at your own risk.

It would be great to hear from you if this library was of use in your research.

Email bugs, comments, and suggestions to [email protected].