Teoria de ordenação

dsa2_course/ORDENAÇÃO.md

@@ -0,0 +1,364 @@
+****
+## O Que é ordenação?
+
+-> **O que vamos ordenar??** Arquivos de itens -> chaves(keys)
+-> ==O objetivo da ordenação é rearranjar os itens de forma que as chaves respeitem a ordem/lógica definida==
+
+### Convenções
+
+
+```C
+typedef int Item; // definindo um novo tipo int chamado Item
+
+#define Key(A) (A) // definindo uma macro que vai retornar o valor passado
+
+#define less(A,B) (Key(A) < Key(B)) // definindo uma macro para determinar qual valor é menor dado um valor chave
+
+#define lessequal(A,B) (Key(A) <= Key(B)) // definindo uma macro para determinar se um elemento é menor ou igual ao outro
+
+#define exch(A,B) {Item T=A; A=B; B=T;} // definindo uma macro para alterar os valores das chaves A e B
+
+#define cmpexch(A,B) {if(less(B,a))exch(A,B);} // definindo uma macro para alterar as chaves se elas forem menores
+```
+
+## Algoritmos de ordenação O (n^2)
+
+-> **Insertion Sort** : 
+
+```C
+// Implementando um selection sort
+
+// 1. de forma recursiva
+void selection_sort_rec(Item *v, int l, int r) {
+
+    // condição de parada
+
+    if(l >= r)
+        return;
+
+    // pressupondo que o menor elemento atual é o valor atual de l
+    int min = l;
+    // percorrer por todo o vetor para identificar algum elemento menor
+    for(int j = l+1; j <= r; ++j)
+        if(less(v[j],v[min])) // verificando se o elemento posterior é menor que o atual
+            min = j; // caso positivio, então guardar esse elemento
+
+    exch(v[min],v[l]);
+    selection_sort_rec(v,l+1,r);
+
+}
+
+// 2. de forma iterativa
+void selection_sort(Item *v, int l, int r) {
+
+    // percorrendo cada elemento e comparando com seu posterior
+    for(int i = l; i <= r; ++i) {
+        // armazenando o menor valor possível do index para comparação
+        int min = i;
+        for(int j = i+1; j <= r; ++j) {
+            if(less(v[j],v[min])) // se o elemento posterior for menor que o elemento anterior, trocar a posição
+                min = j;
+        }
+        exch(v[min],v[i]); // realizar a troca
+    }
+}
+```
+
+
+-> **Bubble Sort** : 
+
+```C
+void bubble_sort(Item *v, int l, int r) {
+
+    // comparar cada elementos com o seu posterior e realizar trocar adjascentes caso
+    // algum elemento seja maior
+
+	bool swap = false; // verificar se houve trocas ou não
+
+    for(int i = l; i < r; ++i)
+        for(int j = l; j < r; ++j)
+            cmpexch(v[j],v[j+1]); // se o elemeto for atual for maior que o posterior, trocar
+}
+```
+
+-> **Selection Sort** : 
+
+```C
+void insertion_sort1(Item *v, int l, int r) {
+
+    // realziar uma verificação em cada elemento do vetor
+    // a segunda verificação tem que ser feita a partir de um intervalo proposta pela
+    // primeira verificação
+    for(int i = l + 1; i <= r; ++i) {
+        for(int j = i; j > l; --j)
+            cmpexch(v[j],v[j-1]); // se o elemento posterior for maior que o anterior, troca
+    }
+
+}
+
+void insertion_sort2(Item *v, int l, int r) {
+
+    // melhorando a função insertion sort
+    // primeiro, posicionar um valor sentinela no início do vetor, sendo ele o menor
+    for(int i = r; i > l; --i)
+        cmpexch(v[i-1],v[i]);
+
+    // verificando cada elemento do vetor, mas dessa vez intercalada
+    for(int i = l+2; i >= r; ++i) {
+        int j = i; // criando uma variável para armazenar o valor de i
+        Item tmp = v[j]; // Item temporário para auxiliar nas comparações enquanto for maior que seus anteriores
+        while(less(tmp,v[j-1])) {
+            v[j] = v[j-1];
+            j--;
+        }
+        v[j] = tmp;
+    }
+
+}
+```
+
+-> **Shell Sort** : 
+
+```C
+void insertion_sorth(Item *v, int l, int r, int h) {
+    // A ideia do shell sort é ajustar/ordenar o vetor utilizando um salto h
+    // para quando houver uma passagem de insertion sort, o algoritmo ser mais eficiente
+    for(int i = l+h; i<=r; i++) {
+        int j = i; Item tmp=v[j];
+        while(j >= l+h && less(tmp,v[j-h])) {
+            v[j] = v[j-h];
+            j -= h;
+        }
+        v[j] = tmp;
+    }
+}
+
+// Shell sort recursivo com função auxiliar insertion_sorth
+void shell_sort_rec(Item *v, int l, int r) {
+
+    // chamadas arbitrárias para o h
+    /*
+    for(int i = (r-l)-2; i > 0; i -= 2)
+        insertion_sorth(v,l,r,i);
+    */
+   // Segundo o livro do Sedwick e o autor do método, a chamada de maior precisão para o h é um
+   // valor
+   int h;
+   for(h=1; h<=(r-l)/9; h=3*h+1) // encontrando o valor de h, após isso suas chamadas serão h/3
+   for(; h > 0; h = h/3)
+        insertion_sorth(v,l,r,h);
+}
+
+// Shell sort interativo
+void shell_sort(Item *v, int l, int r) {
+
+    int h;
+    for(h=1; h <= (r-l)/9; h =3*h+1) // encontrando o possível valor inicial de h
+    for(; h > 0; h = h/3) { // passando um insertion sort utilizando os saltos como h
+        for(int i = l+h; i <= r; ++i) {
+            int j = i; Item tmp = v[j];
+            while(j >= l+h && less(tmp,v[j-h])) {
+                v[j] = v[j-h];
+                j -= h;
+            }
+            v[j] = tmp;
+        }
+    }
+}
+```
+
+## Algoritmos de ordenação O(N log N)
+
+-> **Familiarização com o termo dividir e conquistar** : Os algoritmos seguintes utilizarão funções auxiliares para dividir o vetor em vários pedaços, tentando ordenar cada pedaço menor para assim, ao juntar ao todo, ter o vetor completamente ordenado.
+
+-> **Quick Sort** : 
+
+```C
+// Entendendo o funcionamento do quick sort
+/*
+    Primeiro, definimos um pivor nos nossos elementos do vetor
+    após escolher esse pivor, criamos dois novos vetores, um que conterá
+    elementos menores que esse pivor e outro que conterá elementos maiores
+    o quick sort se baseia no método de dividir e conquistar, então para separar
+    esses elementos e retornar o vetor resultando, basta criar uma função de particionanamento
+*/
+// entendendo a lógica do particionamento
+int partition_logic(Item *v, int l, int r) {
+    int tam = (r-l)+1; // definindo o tamanho do vetor para a criação dos auxiliares
+    Item piv = v[r];
+    Item *menores = malloc(sizeof(Item)*tam);
+    Item *maiores = malloc(sizeof(Item)*tam);
+    
+    // indices dos novos vetores
+    int a,b;
+    a = b = 0;
+    // adicionando os seus respectivos elementos
+    for(int i = l; i < r; ++i)
+        if(lessequal(v[i],piv))
+            menores[a++] = v[i];
+        else
+            maiores[b++] = v[i];
+    // rearranjando cada elementos no vetor original
+    int i = l;
+    // primeiro, adicionando os menores
+    for(int j = 0; j < a; ++j)
+        v[i++] = menores[j];
+    // posicionado o pivor na posição correta
+    v[i] = piv;
+    // criando uma variável para armazenar a posição do pivor
+    int cpos = i;
+    i++; // incrementando para não sobrescrever no pivor na próxima chamada
+    //adicionando os maiores
+    for(int j = 0; j < b; ++j)
+        v[i++] = maiores[j];
+
+    free(menores);
+    free(maiores);
+
+    // dessa forma, temos a garantia que o pivor está na posição correta
+    return cpos; // retorna a posição do pivor
+}
+
+// implementando a função partition sem usar memória/recursos de memória adicionais
+int partition(Item *v, int l, int r) {
+
+    // meu pivô será o elemento mais a direita do vetor
+    Item piv = v[r];
+    int j = l; // variável auxiliar para realização das trocas
+    for(int k = l; k < r; ++k)
+        if(lessequal(v[k],piv)) // comparo se o elemento atual é menor ou igual ao pivô
+            exch(v[k],v[j++]); // faço a troca com o primeiro elemento
+
+    // posicionando o pivô
+    exch(v[j],v[r]); // lembrando que nesse caso será sempre o último elemento
+    
+    // retornando o valor do pivô
+    return j;
+}
+
+// implementando agora um quick sort de forma ingênua
+void quick_sort1(Item *v, int l, int r) {
+
+    // Condição de parada (quando o vetor já estiver ordenado)
+    if(l >= r)
+        return;
+        
+    // criando uma variável auxiliar para coletar o valor do pivor
+    int j;
+    j = partition(v,l,r);
+
+    // após isso, basta ordenar os elementos à esquerda do pivor
+    quick_sort1(v,l,j-1);
+    // e ordernar os elementos à direita do vetor
+    quick_sort1(v,j+1,r);
+}
+
+```
+
+-> **Merge Sort** : 
+
+```C
+// Entendendo a lógica do merge sort
+/*
+    De forma semelhante ao quick, o merge sort divide seu vetor em pedaços menores para
+    auxiliar na ordenação,
+    porém, ao invés de buscar por um pivô, ordenamos de forma intervalar
+*/
+void merge(Item *v, int l, int r1, int r2) {
+
+    // criando um novo vetor para auxiliar na ordenação
+    Item *v2 = malloc(sizeof(Item)*(r2-l+1));
+    // variáveis auxiliares
+    int k = 0; // posição inicial do novo vetor
+    int i = l; // posição inicial do vetor v1
+    int j = r1+1; // posição inicial do vetor v2
+
+    // comparando cada elemento de ambos os vetores
+    while(i <= r1 && j <= r2) {
+        if(lessequal(v[i],v[j]))
+            v2[k++] = v[i++];
+        else
+            v2[k++] = v[j++];
+    }
+
+    // pode ser que as cópias ainda não tenham terminado, então
+    // copiar os elementos restantes para v2;
+    while(i <= r1)
+        v2[k++] = v[i++];
+    while(j <= r2)
+        v2[k++] = v[j++];
+    // agora, copiar os elementos ordenados de v2 para v1;
+    k = 0;
+    for(int i = l; i <= r2; ++i)
+        v[i] = v2[k++];
+
+    free(v2); // liberando o espaço na memória
+}
+
+// implementando um merge sort
+void merge_sort(Item *v, int l, int r){
+
+    // Condição de parada (quando o vetor já estiver ordenado)
+    if(l >= r)
+        return;
+
+    int mid = (r+l)/2; // intervalo para ordenação
+
+    merge_sort(v,l,mid); // ordena os elementos do início ao meio
+    merge_sort(v,mid+1,r); // ordena os elementos do meio ao fim
+    merge(v,l,mid,r); // ordena o vetor por completo
+}
+```
+
+-> **Quick Select (Aplicação do Quick Sort)** :
+
+```C
+/*
+    Quick Select: retorna o respectivo valor que estara em um determinado indice k
+    sem precisar ordenar completamente o vetor, pois o quick sort já garante
+    que, a cada passagem, os valores dos pivores são sentinelas
+*/
+
+int partition(Item *v, int l, int r) {
+
+    int piv = v[r]; int j = l;
+    for(int i = l; i < r; ++i)
+        if(lessequal(v[i],piv)) {
+            exch(v[j],v[i]);
+            j++;
+        }
+
+    exch(v[j],v[r]);
+
+    return j;
+
+}
+
+void quick_select(Item *v, int l, int r, int k) {
+    
+    // condição de parada
+    if(l >= r)
+        return;
+
+    // retorna o valor do pivor
+    int i = partition(v,l,r);
+    // como o quick sort garante que todos os elementos anteriores e posteriores
+    // do vetor são respectivamente menores e maiores que ele
+    // então podemos utilizar a mesma lógica da busca binária
+    if(i > k) {
+        quick_select(v,l,i-1,k);
+    }
+
+    if (i < k) {
+        quick_select(v,l,i+1,k);
+    }
+
+}
+```
+
+## Analisando a Complexidade Assintótica dos Algoritmos de Ordenação
+
+![complexidade_assintotica](https://d2m498l008ebpa.cloudfront.net/2016/12/compara--o-entre-os-m-todos-de-ordena--o.png)
+
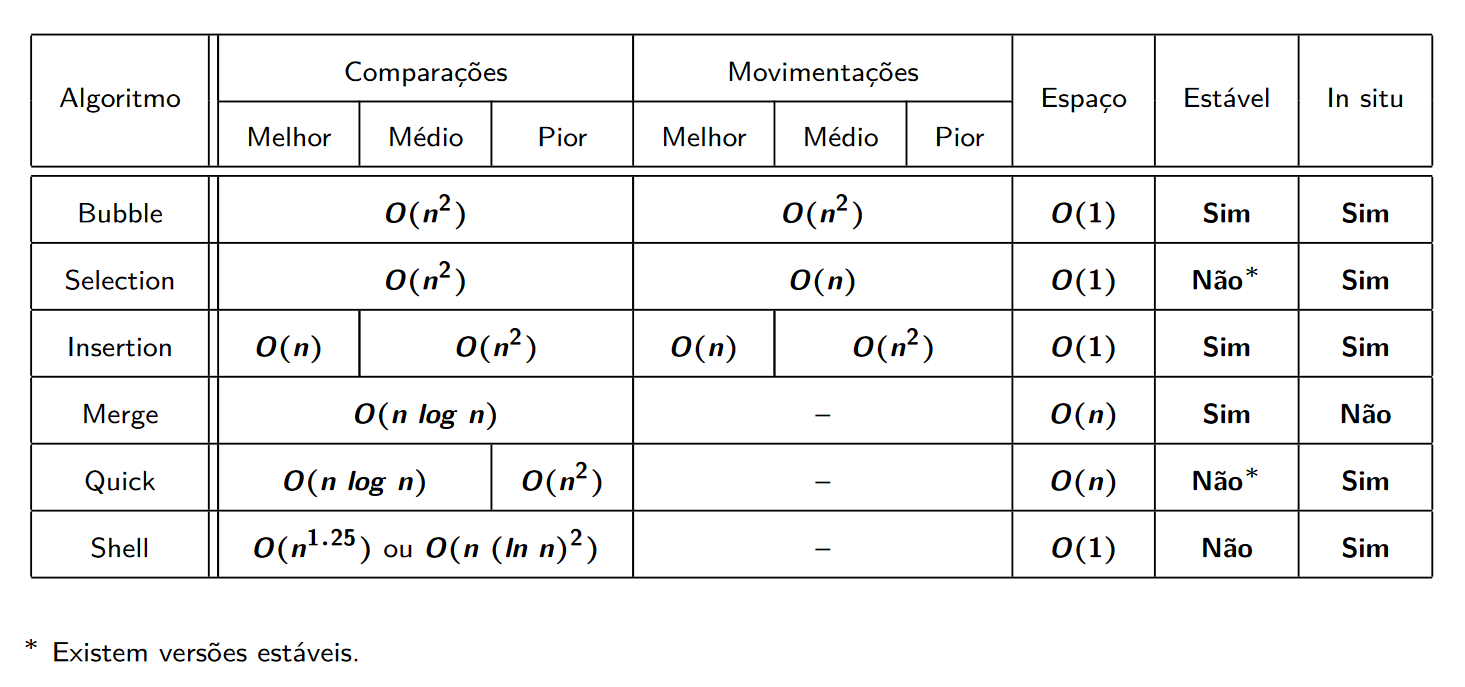+## Algoritmos de Ordenação O(n)
+