论文:基于数字光栅投影的结构光三维测量技术与系统研究 [博]
作者:李中伟 华中科技大学 2007
功能:相移法:多频外差(三频N步相移法)
 |
|---|
| 图1 待写入投影仪的理想N步相移条纹 |
通常对于
-
$A$ :背景光强 -
$B$ :调制强度 -
$x$ :像素点横向坐标 -
$\varphi (x)$ :相移值
 |
|---|
| 图2 相机拍摄到的实际 N 步相移条纹 |
由于物体表面高度、反射率不同,因此相机拍摄到某个像素点
三角函数的合角、差角公式: $$ \begin{gathered} \sin \left( {\alpha + \beta } \right) = \sin \alpha \cos \beta + \sin \beta \cos \alpha \hfill \ \sin \left( {\alpha - \beta } \right) = \sin \alpha \cos \beta - \sin \beta \cos \alpha \hfill \ \cos \left( {\alpha + \beta } \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \hfill \ \cos \left( {\alpha - \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \hfill \ \end{gathered} $$
求解过程如下,将方程进行化简: $$ \begin{array}{l} {I_k}\left( {x,y} \right)
&= A\left( {x,y} \right) + B\left( {x,y} \right)\cos \left[ {\varphi \left( {x,y} \right) + \frac{{2k\pi }}{N}} \right] \hfill \
&= A\left( {x,y} \right) + B\left( {x,y} \right)\left[ {\cos \left( {\varphi \left( {x,y} \right)} \right)\cos \left( {\frac{{2k\pi }}{N}} \right) - \sin \left( {\varphi \left( {x,y} \right)} \right)\sin \left( {\frac{{2k\pi }}{N}} \right)} \right] \hfill \
&= A\left( {x,y} \right) + \cos \left( {\frac{{2k\pi }}{N}} \right) \cdot \underbrace {B\left( {x,y} \right)\cos \left( {\varphi \left( {x,y} \right)} \right)}{{B_1}\left( {x,y} \right)} - \sin \left( {\frac{{2k\pi }}{N}} \right) \cdot \underbrace {B\left( {x,y} \right)\sin \left( {\varphi \left( x,y \right)} \right)}{{B_2}\left( {x,y} \right)} \hfill \
\end{array} \label{5}
$$
式子中,$A(x,y)、B_1{(x,y)}、B_2{(x,y)}$ 是未知数,而
超定方程解
考虑线性方程: $$ Ax=b \ A \in {\mathbb{R}{m \times n}},x \in {\mathbb{R}{n \times 1}},b \in {\mathbb{R}_{m \times 1}} $$
$m$ 个方程求解$n$ 个未知数,有三种情况:
$m=n$ ,且$A$ 为满秩矩阵,则有唯一解:$x= A^{-1} b$$m < n$ ,欠定问题,无数解(可以看相应教材)$m > n$ ,约束的个数大于未知数个数,称为超定问题通常我们遇到的都是超定问题,此时
$Ax = b$ 不存在解,转而求误差最小,即最小二乘问题: $$ J(x)=\min \left| {Ax - b} \right|_2^2 $$ 矩阵转置 $$ (A^T)^T=A \ (A+B)^T = A^T + B^T\ (AB)^T = B^T A^T $$ 对$l2$ 范式展开: $$ \begin{array}{l} {\left( {Ax - b} \right)^T}\left( {Ax - b} \right) &= \left( {{x^T}{A^T} - {b^T}} \right)\left( {Ax - b} \right) \hfill \ &= {x^T}{A^T}Ax - {b^T}Ax - {x^T}{A^T}b + {b^T}b \hfill \ &= {x^T}{A^T}Ax - 2{b^T}Ax + {b^T}b \hfill \ \end{array} $$ 式子中:$b^TAx$ 和$x^TA^Tb$ 互为转置,且都为标量,因此相等。向量求偏导公式: $$ \begin{array}{l} \frac{{\partial \left( {{A^T}\beta } \right)}}{{\partial \beta }} &= A \hfill \ \frac{{\partial \left( {{\beta ^T}A\beta } \right)}}{{\partial \beta }} &= \left( {A + {A^T}} \right)\beta = 2A\beta \left( {A是对称矩阵} \right) \hfill \ \end{array} $$
$J(x)$ 是凸函数(二阶导数非负),我们令一阶导数为0,可以得到: $$ \frac{{\partial \left( {{x^T}{A^T}Ax - 2{b^T}Ax + {b^T}b} \right)}}{{\partial x}}= 2\left( {{A^T}A} \right)x - 2{\left( {{b^T}A} \right)^T}
= 2{A^T}Ax - 2{A^T}b = 0 $$ 进而方程的解: $$ x=(A^TA)^{-1}A^Tb $$
其中:$(A^TA)^{-1}A^T$ 又称为伪逆,因为它和方阵的
$x = A^{-1} b$ 的作用是一样的由于这里需要取逆操作,计算量较大,并且
$A^TA$ 还有可能存在“病态”,甚至不可逆的情况,因此实际情况更多的是用 SVD 方法来求解超定方程,也就是最小二乘问题。
根据线性代数知识,超定方程的解:
$$
x=(A^TA)^{-1}A^Tb
$$
将式子代入,先计算
&= \left[ {\begin{array}{*{20}{c}} 1& \cdots &1& \cdots &1 \ {\cos \left( {\frac{{0 \cdot 2\pi }}{N}} \right)}& \cdots &{\cos \left( {\frac{{k \cdot 2\pi }}{N}} \right)}& \cdots &{\cos \left( {\frac{{\left( {N - 1} \right) \cdot 2\pi }}{N}} \right)} \ { - \sin \left( {\frac{{0 \cdot 2\pi }}{N}} \right)}& \cdots &{ - \sin \left( {\frac{{k \cdot 2\pi }}{N}} \right)}& \cdots &{ - \sin \left( {\frac{{\left( {N - 1} \right) \cdot 2\pi }}{N}} \right)} \end{array}} \right] \hfill \
&\times \left[ {\begin{array}{*{20}{c}} 1&{\cos \left( {\frac{{0 \cdot 2\pi }}{N}} \right)}&{ - \sin \left( {\frac{{0 \cdot 2\pi }}{N}} \right)} \ \vdots & \vdots & \vdots \ 1&{\cos \left( {\frac{{k \cdot 2\pi }}{N}} \right)}&{ - \sin \left( {\frac{{k \cdot 2\pi }}{N}} \right)} \ \vdots & \vdots & \vdots \ 1&{\cos \left( {\frac{{\left( {N - 1} \right) \cdot 2\pi }}{N}} \right)}&{ - \sin \left( {\frac{{\left( {N - 1} \right) \cdot 2\pi }}{N}} \right)} \end{array}} \right] \hfill \
&= \left[ {\begin{array}{*{20}{c}} N&{\sum\limits_{k = 0}^{N - 1} {\cos \frac{{2k\pi }}{N}} }&{ - \sum\limits_{k = 0}^{N - 1} {\sin \frac{{2k\pi }}{N}} } \ {\sum\limits_{k = 0}^{N - 1} {\cos \left( {\frac{{2k\pi }}{N}} \right)} }&{\sum\limits_{k = 0}^{N - 1} {{{\cos }^2}\left( {\frac{{2k\pi }}{N}} \right)} }&{ - \sum\limits_{k = 0}^{N - 1} {\sin \left( {\frac{{2k\pi }}{N}} \right)\cos \left( {\frac{{2k\pi }}{N}} \right)} } \ { - \sum\limits_{k = 0}^{ N - 1} {\sin \left( {\frac{{2k\pi }}{N}} \right)} }&{ - \sum\limits_{k = 0}^{N - 1} {\sin \left( {\frac{{2k\pi }}{N}} \right)\cos \left( {\frac{{2k\pi }}{N}} \right)} }&{\sum\limits_{k = 0}^{N - 1} {{{\sin }^2}\left( {\frac{{2k\pi }}{N}} \right)} } \end{array}} \right] \hfill \ \end{array} $$ 可以发现,除了对角线上的元素,边上的元素都是周期性函数,因此只需要计算一个周期($2 \pi$)的即可。我们一个个来计算,例如:
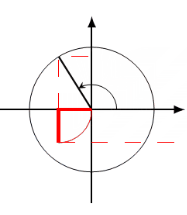 |
|---|
| 图3 余弦函数(积分为零) |
我们将
积化和差: $$ \eqalign{ & \sin \alpha \cos \beta = \frac{1}{2}\left[ {\sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha - \beta } \right)} \right] \cr & \cos \alpha \sin \beta = \frac{1}{2}\left[ {\sin \left( {\alpha + \beta } \right) - \sin \left( {\alpha - \beta } \right)} \right] \cr & \cos \alpha \cos \beta = \frac{1}{2}\left[ {\cos \left( {\alpha + \beta } \right) + \cos \left( {\alpha - \beta } \right)} \right] \cr & \sin \alpha \sin \beta = \frac{1}{2}\left[ {\cos \left( {\alpha + \beta } \right) - \sin \left( {\alpha - \beta } \right)} \right] \cr} $$
对于:
$$
\sum\limits_{k = 0}^{N - 1} {\sin \Delta \varphi } \cos \Delta \varphi = \frac{1}{2}\sum\limits_{k = 0}^{N - 1} {\sin 2} \Delta \varphi = 0
$$
对于:
$$
\begin{gathered}
\sum\limits_{k = 0}^{N - 1} {{{\cos }^2}\Delta {\varphi k} = \sum\limits{k = 0}^{N - 1} {\frac{{1 + \cos 2{\varphi k}}}{2}} } = \sum\limits{k = 0}^{N - 1} {\frac{1}{2} + \frac{{\cos 2{\varphi k}}}{2}} = \frac{N}{2} \hfill \
\sum\limits{k = 0}^{N - 1} {{{\sin }^2}\Delta {\varphi k} = \sum\limits{k = 0}^{N - 1} {\frac{{1 - \cos 2{\varphi k}}}{2}} } = \sum\limits{k = 0}^{N - 1} {\frac{1}{2} - \frac{{\cos 2{\varphi _k}}}{2}} = \frac{N}{2} \hfill \
\end{gathered}
$$
于是
(A^TA) ^ {-1}=\left[ {\begin{array}{{20}{c}} {1/N}&0&0 \ 0&{2/N}&0 \ 0&0&{2/N} \end{array}} \right] $$ 最终$(A^TA)^{-1}A^Tb$ 的结果: $$ \begin{array}{l} {\left( {{A^T}A} \right)^{ - 1}}Ab {\text{ = }}\left[ {\begin{array}{{20}{c}} {1/N}&0&0 \ 0&{2/N}&0 \ 0&0&{2/N} \end{array}} \right] ... \
\times
\left[ {\begin{array}{{20}{c}}
1& \cdots &1& \cdots &1 \
{\cos \left( {\frac{{0 \cdot 2\pi }}{N}} \right)}& \cdots &{\cos \left( {\frac{{k \cdot 2\pi }}{N}} \right)}& \cdots &{\cos \left( {\frac{{(N - 1) \cdot 2\pi }}{N}} \right)} \
{ - \sin \left( {\frac{{0 \cdot 2\pi }}{N}} \right)}& \cdots &{ - \sin \left( {\frac{{k \cdot 2\pi }}{N}} \right)}& \cdots &{ - \sin \left( {\frac{{(N - 1) \cdot 2\pi }}{N}} \right)}
\end{array}} \right]\left[ {\begin{array}{{20}{c}}
{{I_0}\left( {x,y} \right)} \
\vdots \
{{I_k}\left( {x,y} \right)} \
\vdots \
{{I_{N - 1}}\left( {x.y} \right)}
\end{array}} \right] \hfill \
= \left[ {\begin{array}{{20}{c}}
{1/N}&0&0 \
0&{2/N}&0 \
0&0&{2/N}
\end{array}} \right]\left[ {\begin{array}{{20}{c}}
{\sum\limits_{k = 0}^{N - 1} {{I_k}\left( {x,y} \right)} } \
{\sum\limits_{k = 0}^{N - 1} {\cos \left( {\frac{{2k\pi }}{N}} \right){I_k}\left( {x,y} \right)} } \
{\sum\limits_{k = 0}^{N - 1} {\sin \left( {\frac{{2k\pi }}{N}} \right){I_k}\left( {x,y} \right)} }
\end{array}} \right] \hfill \
= \left[ {\begin{array}{*{20}{c}}
{\frac{1}{N}\sum\limits_{k = 0}^{N - 1} {{I_k}\left( {x,y} \right)} } \
{\frac{2}{N}\sum\limits_{k = 0}^{N - 1} {\cos \left( {\frac{{2k\pi }}{N}} \right){I_k}\left( {x,y} \right)} } \
{ - \frac{2}{N}\sum\limits_{k = 0}^{N - 1} {\sin \left( {\frac{{2k\pi }}{N}} \right){I_k}\left( {x,y} \right)} }
\end{array}} \right] \hfill \
\end{array}
$$
即:
$$
\begin{array}{l}
A\left( {x,y} \right) &= \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {{I_k}\left( {x,y} \right)} \hfill \
{B_1}\left( {x,y} \right) &= \frac{2}{N}\sum\limits_{k = 0}^{N - 1} {\cos \left( {\frac{{2k\pi }}{N}} \right){I_k}\left( {x,y} \right)} \hfill \
{B_2}\left( {x,y} \right) &= - \frac{2}{N}\sum\limits_{k = 0}^{N - 1} {\sin \left( {\frac{{2k\pi }}{N}} \right){I_k}\left( {x,y} \right)} \hfill \
\end{array}
$$
由公式
 |
|---|
| 图4 多频外差:原理示意图 |
合成相位
两者的相位差(用蓝色加粗标出),可以增大标记视场: $$ {\phi _{12}}{\text{ = }}\left{ {\begin{array}{*{20}{c}} {{\phi _1} - {\phi _2},\quad {\phi _1} \ge {\phi _2}} \ {2\pi - \left( {{\phi _2} - {\phi _1}} \right), \quad {\phi _1} > {\phi _2}} \end{array}} \right. $$ 很直观地看出,它实际是绝对相位的相减: $$ \begin{array}{l} {\varphi _{12}} &= {\varphi _1} - {\varphi _2} \hfill \ &= \left( {{\phi _1} + 2\pi {n_1}} \right) - \left( {{\phi _2} + 2\pi {n_2}} \right) \hfill \ &= \left( {{\phi _1} - {\phi _2}} \right) + 2\pi \left( {{n_1} - {n_2}} \right) \hfill \ \end{array} $$
其中:$n_1, n_2$ 分别是条纹阶次,$\varphi_{12} ,\varphi_1,\varphi_2$ 代表绝对相位。 结合图4,依次代入即可得到相位差公式。
合成波长
下面来计算合成的波长
如图4的下半段的前面部分,同样也有: $$ \varphi_{12} = \lambda \times \frac{2 \pi}{\lambda_{12}} $$ 反过来: $$ \lambda_{12} = \lambda \times \frac{2 \pi}{\varphi_{12}} = \frac{\lambda_1 \lambda_2}{\lambda_2 - \lambda_1} $$ 参照文献 [1] 的做法,频率选取: $$ {\lambda _1} = 1/70,{\lambda _2} = 1/64,{\lambda _3} = 1/59 $$ 计算如下: $$ {\lambda _{12}}{\rm{ = }}\frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _2} - {\lambda _1}}}{\rm{ = }}\frac{1}{6},
{\lambda _{23}}{\rm{ = }}\frac{{{\lambda _2}{\lambda _3}}}{{{\lambda _3} - {\lambda _2}}}{\rm{ = }}\frac{1}{5},
{\lambda _{123}}{\rm{ = }}\frac{{{\lambda _{12}}{\lambda _{23}}}}{{{\lambda _{23}} - {\lambda _{12}}}}{\rm{ = }}1 $$
注:对比之前频率
在相移法+格雷码中,通常我们也选择这样的实现,因为一个周期是一个整数像素。
相应的视场合成公式: $$ T_{12} = \frac{T_1 \times T_2}{T_1 - T_2} $$
相应的视场计算: $$
$$
而李中伟实现的频率
如果参照之前的定义,其实际周期是:$W/T=W\lambda$,那么多频外差合成公式: $$ W{\lambda _{12}} = \frac{{\left( {W{\lambda _1}} \right) \times \left( {W{\lambda _2}} \right)}}{{\left( {W{\lambda _1}} \right) - \left( {W{\lambda _2}} \right)}} \to {\lambda _{12}} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} - {\lambda _2}}} $$
由于
- 前者一个周期经历:$T_p$ 个像素,后者实际上一个周期占据的像素:$\frac{W}{T_b}$,这意味着后者无论视场变化多大,都可以自适应适配。
- 由于生成条纹中相位
$\varphi(x)$ 的公式不同,因此两者的多频合成公式略有不同。前者三频外差时需要进行归一化,并且加入误差项。 - 通常来说,频率越高(例如
$1/70 \ge 1 / 22$ )相位误差越小(在$1/28,1/26,1/24$中,我们甚至需要加入误差项,才能保证解出的相位平滑),但是在相位偏折术,由于相机是离焦的,因为采样误差的关系,条纹频率不能选择太高。
回复关键字下载代码,更多的代码请参考课程《从零搭建一套结构光3D重建系统[理论+源码+实践]。课程大纲如下(链接):
提供的源代码:
另外还有:互补格雷码实现、以及最新的一些论文,提供答疑。