Least squares fitting is a underlying method for numerous applications, the most common one being linear regression. It consists in finding the parameters vector β° which minimizes ‖ε‖₂ in the equation y = Xβ + ε, where X is the design matrix, y the observation vector, and ε the error vector.
Since it is a fundamental algorithm, a number of Python 3 implementations exist, with different feature sets and performance, such as: numpy.linalg.lstsq, scipy.stats.linregress, sklearn.linear_model.LinearRegression and statsmodel.OLS.
However, the current available libraries are not designed to work on a large quantity of simultaneous problems, for example solving a least square problem for each pixel of an image. Iterating over a large number of small problems is inefficient. Moreover, when doing linear regression, it is often tedious to build the design matrix X.
The goal of multilstsq is to work on arrays of problems, with good performance, low memory requirements, reliability and flexibility. It also provides a way to automate the construction of the relevant structures (mostly the design matrix), using a model given as a string. It however does not strive to be a complete statistical library such as what would be provided by statsmodel or the language R.
To reach these goals, multilstsq uses the following techniques:
- It is possible to compute
β°=(XᵀX)⁻¹Xᵀyincrementally, due to the linearity ofXᵀXandXᵀy, by providing data in chunks. - Inverting
XᵀXis done by explicit formulas when the dimension is small. This has the advantage of being vector operations which can be applied simultaneously on all problems. - Masked data are handled as lines of zeros in the design matrix and the observation, which in fact have no effect. This allows adding different amount of data in different subproblems.
- For regression, an expression evaluator is implemented, which converts the input model from the user (for example
b0+b1*x0) into the complex expression needed to build the design matrix from the vectorXprovided by the user. In that example, it is:np.concatenate([np.ones(o_dim)[(..., np.newaxis)], ((X)[..., :, 0])[(..., np.newaxis)]]). This expression evaluator also may be useful for other purposes in other libraries.
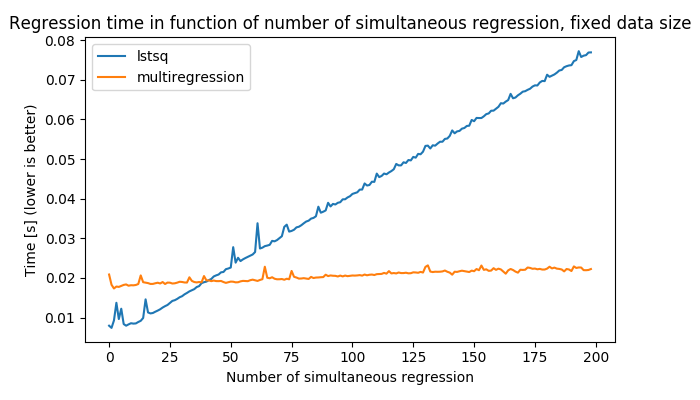
As shown in the following figure, this ensures the algorithm has good performance compared to a loop:
import numpy as np
from multilstsq import MultiRegression
x1 = np.array([1.47, 1.50, 1.52, 1.55, 1.57, 1.60, 1.63, 1.65, 1.68, 1.70, 1.73, 1.75, 1.78, 1.80, 1.83])
y1 = np.array([52.21, 53.12, 54.48, 55.84, 57.20, 58.57, 59.93, 61.29, 63.11, 64.47, 66.28, 68.10, 69.92, 72.19, 74.46])
x2 = np.arange(10)
y2 = np.arange(10)
X = np.ma.masked_all((2, max(len(x1), len(x2)), 1))
y = np.ma.masked_all((2, max(len(x1), len(x2)), 1))
X[0, :len(x1), 0] = x1
X[1, :len(x2), 0] = x2
y[0, :len(y1), 0] = y1
y[1, :len(y2), 0] = y2
mr = MultiRegression((2,), 'b0 + b1*x0 + b2*(x0**2)')
mr.add_data(X,y)
mr.switch_to_variance()
mr.add_data(X,y)
print(mr.beta)
#Identify parameter names in the parameter vector
print(mr.beta_names)
#Get the covariance matrix for the first problem
print(mr.variance[0])
#Get the expression to predict for the first problem
expr = mr.get_expr_for_idx((0,))
#Evaluate at x=1.79
print(expr(1.79))The nice thing about this module is that it is possible to change the model by only changing the line instanciating the MultiRegression object. For example, for a quadratic regression:
mr = MultiRegression((2,), 'b0 + b1*x0 + b2*(x0**2)')Documentation is available at http://multilstsq.readthedocs.io/
Please post issues and pull requests on github. Alternatively, you can also send your patches by email.
The following tools are used to ensure good code quality:
| Tool | Status |
|---|---|
| travis-ci | |
| AppVeyor | |
| Coveralls |