This repo contains the VNN-COMP 2024 entry of the neural network verifier α,β-CROWN (alpha-beta-CROWN). This is not an official release of alpha-beta-CROWN. It is solely for reproducing results in VNN-COMP 2024. For other purposes, please use the official release instead.
This version contains new algorithms from papers under review. If you are reviewing any paper written recently, they may refer to and compare to the previous version of alpha-beta-CROWN without these new and unpublised algorithms.
This VNN-COMP 2024 entry of alpha-beta-CROWN is prepared by a team:
VNN-COMP 2024 team co-leaders:
- Zhouxing Shi (UCLA) and Huan Zhang (UIUC)
VNN-COMP 2024 team members:
- Duo Zhou (UIUC)
- Jorge Chavez (UIUC)
- Xiangru Zhong (UIUC)
- Hongji Xu (Duke, working as an intern supervised by Prof. Huan Zhang at UIUC)
- Kaidi Xu (Drexel)
- Hao Chen (UIUC)
The team acknowledges the contributions from all recent contributors.
This repo also includes the full source code of auto_LiRPA, since alpha-beta-CROWN and auto_LiRPA are internally developed together, although they are released as two separate packages to enable better community reuse of the linear bound propagation procedures in other verifiers.
The original README is included below.
α,β-CROWN (alpha-beta-CROWN): A Fast and Scalable Neural Network Verifier with Efficient Bound Propagation
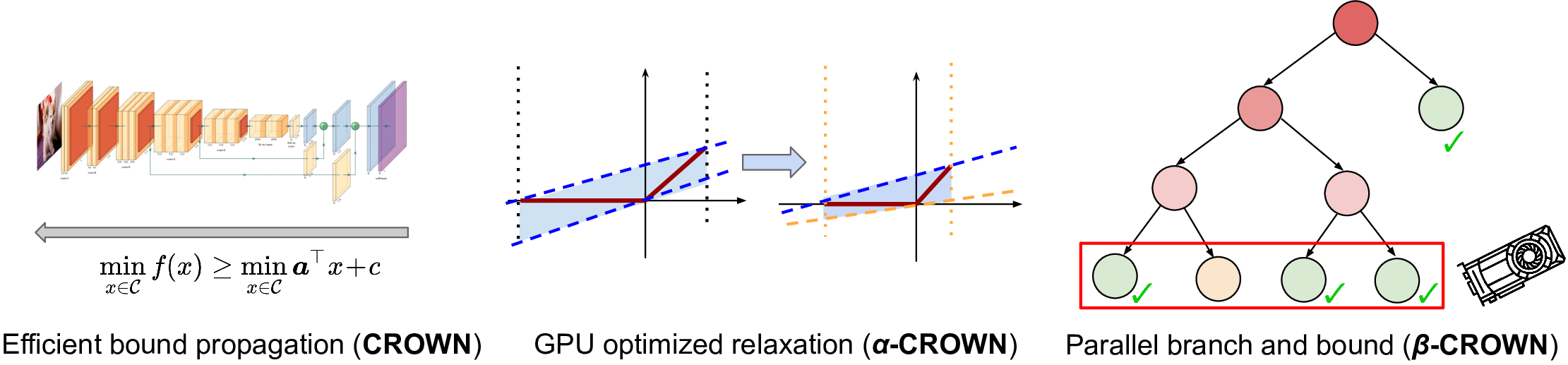
α,β-CROWN (alpha-beta-CROWN) is a neural network verifier based on an efficient linear bound propagation framework and branch and bound. It can be accelerated efficiently on GPUs and can scale to relatively large convolutional networks (e.g., millions of parameters). It also supports a wide range of neural network architectures (e.g., CNN, ResNet, and various activation functions), thanks to the versatile auto_LiRPA library developed by us. α,β-CROWN can provide provable robustness guarantees against adversarial attacks and can also verify other general properties of neural networks, such as Lyapunov stability in control.
α,β-CROWN is the winning verifier in VNN-COMP 2021, VNN-COMP 2022, and VNN-COMP 2023 (International Verification of Neural Networks Competition) with the highest total score, outperforming many other neural network verifiers on a wide range of benchmarks over 3 years. Details of competition results can be found in VNN-COMP 2021 slides, report, VNN-COMP 2022 report, VNN-COMP 2023 slides and report.
The α,β-CROWN team is created and led by Prof. Huan Zhang at UIUC with contributions from multiple institutions. See the list of contributors below. α,β-CROWN combines our efforts in neural network verification in a series of papers building up the bound propagation framework since 2018. See Publications below.
Our verifier consists of the following core algorithms:
- CROWN (Zhang et al. 2018): the basic linear bound propagation framework for neural networks.
- α-CROWN (Xu et al., 2021): incomplete verification with gradient optimized bound propagation.
- β-CROWN (Wang et al. 2021): complete verification with bound propagation and branch and bound for ReLU networks.
- GenBaB (Shi et al. 2024): Branch and bound for general nonlinear functions.
- GCP-CROWN (Zhang et al. 2022): CROWN-like bound propagation with general cutting plane constraints.
- BaB-Attack (Zhang et al. 2022): Branch and bound based adversarial attack for tackling hard instances.
- MIP (Tjeng et al., 2017): mixed integer programming (slow but can be useful on small models).
- INVPROP (Kotha et al. 2023): tightens bounds with constraints on model outputs, and computes provable preimages for neural networks.
The bound propagation engine in α,β-CROWN is implemented as a separate library, auto_LiRPA (Xu et al. 2020), for computing symbolic bounds for general computational graphs. We support these neural network architectures:
- Layers: fully connected (FC), convolutional (CNN), pooling (average pool and max pool), transposed convolution
- Activation functions or nonlinear functions: ReLU, sigmoid, tanh, arctan, sin, cos, tan, gelu, pow, multiplication and self-attention
- Residual connections, Transformers, LSTMs, and other irregular graphs
We support the following verification specifications:
- Lp norm perturbation (p=1,2,infinity, as often used in robustness verification)
- VNNLIB format input (at most two layers of AND/OR clause, as used in VNN-COMP)
- Any linear specifications on neural network output (which can be added as a linear layer)
We provide many example configurations in
complete_verifier/exp_configs directory to
start with:
- MNIST: MLP and CNN models
- CIFAR-10, CIFAR-100, TinyImageNet: CNN and ResNet models with high dimensional inputs
- ACASXu, NN4sys, ML4ACOPF and other relatively low-dimensional models
- Stability verification of NN controllers: Verified-Intelligence/Lyapunov_Stable_NN_Controllers
See the Guide on Algorithm Selection to find the most suitable example to get started.
α,β-CROWN is tested on Python 3.11 and PyTorch 2.2.1 (lower versions, including Python 3.7 and PyTorch 1.11, may also work). It can be installed easily into a conda environment. If you don't have conda, you can install miniconda.
Clone our verifier including the auto_LiRPA submodule:
git clone --recursive https://github.com/Verified-Intelligence/alpha-beta-CROWN.gitSetup the conda environment:
# Remove the old environment, if necessary.
conda deactivate; conda env remove --name alpha-beta-crown
# install all dependents into the alpha-beta-crown environment
conda env create -f complete_verifier/environment.yaml --name alpha-beta-crown
# activate the environment
conda activate alpha-beta-crownIf you use the CROWN, α-CROWN and/or β-CROWN verifiers (which cover the most use
cases), a Gurobi license is not needed. If you want to use MIP-based
verification algorithms (which are feasible only for small models), you need to
install a Gurobi license with the grbgetkey command. If you don't have
access to a license, by default, the above installation procedure includes a
free and restricted license, which is actually sufficient for many relatively
small NNs. If you use the GCP-CROWN verifier, an installation of IBM CPlex
solver is required. Instructions to install the CPlex solver can be found
in the VNN-COMP benchmark instructions
or the GCP-CROWN instructions.
If you prefer to install packages manually rather than using a prepared conda environment, you can refer to this installation script.
If you want to run α,β-CROWN verifier on the VNN-COMP benchmarks (e.g., to make a comparison to a new verifier), you can follow this guide.
We provide a unified front-end for the verifier, abcrown.py. All parameters
for the verifier are defined in a yaml config file. For example, to run
robustness verification on a CIFAR-10 ResNet network, you just run:
conda activate alpha-beta-crown # activate the conda environment
cd complete_verifier
python abcrown.py --config exp_configs/tutorial_examples/cifar_resnet_2b.yamlYou can find explanations for the most useful parameters in this example config
file. For detailed usage
and tutorial examples, please see the Usage
Documentation. We also provide a
large range of examples in the
complete_verifier/exp_configs folder.
If you use our verifier in your work, please kindly cite our papers:
- CROWN (Zhang et al., 2018), auto_LiRPA (Xu et al., 2020), α-CROWN (Xu et al., 2021), β-CROWN (Wang et al., 2021), GenBaB (Shi et al. 2024), and GCP-CROWN (Zhang et al., 2022).
- Kotha et al., 2023 if you use constraints on the outputs of neural networks.
- Salman et al., 2019, if your work involves the convex relaxation of the NN verification.
- Zhang et al. 2022, if you use our branch-and-bound based adversarial attack (falsifier).
α,β-CROWN combines our existing efforts on neural network verification:
-
CROWN (Zhang et al. NeurIPS 2018) is a very efficient bound propagation based verification algorithm. CROWN propagates a linear inequality backward through the network and utilizes linear bounds to relax activation functions.
-
The "convex relaxation barrier" (Salman et al., NeurIPS 2019) paper concludes that optimizing the ReLU relaxation allows CROWN (referred to as a "greedy" primal space solver) to achieve the same solution as linear programming (LP) based verifiers.
-
LiRPA (Xu et al., NeurIPS 2020) is a generalization of CROWN on general computational graphs and we also provide an efficient GPU implementation, the auto_LiRPA library.
-
α-CROWN (sometimes referred to as optimized CROWN or optimized LiRPA) is used in the Fast-and-Complete verifier (Xu et al., ICLR 2021), which jointly optimizes intermediate layer bounds and final layer bounds in CROWN via variable α. α-CROWN typically has greater power than LP since LP cannot cheaply tighten intermediate layer bounds.
-
β-CROWN (Wang et al., NeurIPS 2021) incorporates ReLU split constraints in branch and bound (BaB) into the CROWN bound propagation procedure via an additional optimizable parameter β. The combination of efficient and GPU-accelerated bound propagation with branch and bound produces a powerful and scalable neural network verifier.
-
BaB-Attack (Zhang et al., ICML 2022) is a strong falsifier (adversarial attack) based on branch and bound, which can find adversarial examples for hard instances where gradient or input-space-search based methods cannot succeed.
-
GCP-CROWN (Zhang et al., NeurIPS 2022) enables the use of general cutting planes methods for neural network verification in a GPU-accelerated and very efficient bound propagation framework. Cutting planes can significantly strengthen bound tightness.
-
GenBaB (Shi et al. 2024) enables branch-and-bound based verification for non-ReLU and general nonlinear functions, achieving significant improvements on verifying neural networks with non-ReLU activation functions such as Transformer and LSTM networks, and models that consist of neural networks and additional nonlinear operations such as ML for AC Optimal Power Flow.
-
INVPROP (Kotha et al., NeurIPS 2023) handles constraints on the outputs of neural networks which enables tight and provable bounds on the preimage of a neural network. We demonstrated several applications, including OOD detection, backward reachability analysis for NN-controlled systems, and tightening bounds for robustness verification.
We provide bibtex entries below:
@article{zhang2018efficient,
title={Efficient Neural Network Robustness Certification with General Activation Functions},
author={Zhang, Huan and Weng, Tsui-Wei and Chen, Pin-Yu and Hsieh, Cho-Jui and Daniel, Luca},
journal={Advances in Neural Information Processing Systems},
volume={31},
pages={4939--4948},
year={2018},
url={https://arxiv.org/pdf/1811.00866.pdf}
}
@article{xu2020automatic,
title={Automatic perturbation analysis for scalable certified robustness and beyond},
author={Xu, Kaidi and Shi, Zhouxing and Zhang, Huan and Wang, Yihan and Chang, Kai-Wei and Huang, Minlie and Kailkhura, Bhavya and Lin, Xue and Hsieh, Cho-Jui},
journal={Advances in Neural Information Processing Systems},
volume={33},
year={2020}
}
@article{salman2019convex,
title={A Convex Relaxation Barrier to Tight Robustness Verification of Neural Networks},
author={Salman, Hadi and Yang, Greg and Zhang, Huan and Hsieh, Cho-Jui and Zhang, Pengchuan},
journal={Advances in Neural Information Processing Systems},
volume={32},
pages={9835--9846},
year={2019}
}
@inproceedings{xu2021fast,
title={{Fast and Complete}: Enabling Complete Neural Network Verification with Rapid and Massively Parallel Incomplete Verifiers},
author={Kaidi Xu and Huan Zhang and Shiqi Wang and Yihan Wang and Suman Jana and Xue Lin and Cho-Jui Hsieh},
booktitle={International Conference on Learning Representations},
year={2021},
url={https://openreview.net/forum?id=nVZtXBI6LNn}
}
@article{wang2021beta,
title={{Beta-CROWN}: Efficient bound propagation with per-neuron split constraints for complete and incomplete neural network verification},
author={Wang, Shiqi and Zhang, Huan and Xu, Kaidi and Lin, Xue and Jana, Suman and Hsieh, Cho-Jui and Kolter, J Zico},
journal={Advances in Neural Information Processing Systems},
volume={34},
year={2021}
}
@InProceedings{zhang22babattack,
title = {A Branch and Bound Framework for Stronger Adversarial Attacks of {R}e{LU} Networks},
author = {Zhang, Huan and Wang, Shiqi and Xu, Kaidi and Wang, Yihan and Jana, Suman and Hsieh, Cho-Jui and Kolter, Zico},
booktitle = {Proceedings of the 39th International Conference on Machine Learning},
volume = {162},
pages = {26591--26604},
year = {2022},
}
@article{zhang2022general,
title={General Cutting Planes for Bound-Propagation-Based Neural Network Verification},
author={Zhang, Huan and Wang, Shiqi and Xu, Kaidi and Li, Linyi and Li, Bo and Jana, Suman and Hsieh, Cho-Jui and Kolter, J Zico},
journal={Advances in Neural Information Processing Systems},
year={2022}
}
@article{shi2024genbab,
title={Neural Network Verification with Branch-and-Bound for General Nonlinearities},
author={Shi, Zhouxing and Jin, Qirui and Kolter, Zico and Jana, Suman and Hsieh, Cho-Jui and Zhang, Huan},
journal={arXiv preprint arXiv:2405.21063},
year={2024}
}
@inproceedings{kotha2023provably,
author = {Kotha, Suhas and Brix, Christopher and Kolter, J. Zico and Dvijotham, Krishnamurthy and Zhang, Huan},
booktitle = {Advances in Neural Information Processing Systems},
editor = {A. Oh and T. Neumann and A. Globerson and K. Saenko and M. Hardt and S. Levine},
pages = {80270--80290},
publisher = {Curran Associates, Inc.},
title = {Provably Bounding Neural Network Preimages},
url = {https://proceedings.neurips.cc/paper_files/paper/2023/file/fe061ec0ae03c5cf5b5323a2b9121bfd-Paper-Conference.pdf},
volume = {36},
year = {2023}
}
The α,β-CROWN verifier is currently being developed by a multi-institutional team:
Team lead:
- Huan Zhang ([email protected]), UIUC
Current developers:
- Zhouxing Shi ([email protected]), UCLA
- Christopher Brix ([email protected]), RWTH Aachen University
- Kaidi Xu ([email protected]), Drexel University
- Xiangru Zhong ([email protected]), Sun Yat-sen University
- Qirui Jin ([email protected]), University of Michigan
- Hao Chen ([email protected]), UIUC
- Hongji Xu ([email protected]), Duke University
Past developers:
- Linyi Li ([email protected]), UIUC
- Zhuolin Yang ([email protected]), UIUC
- Zhuowen Yuan ([email protected]), UIUC
- Shiqi Wang ([email protected]), Columbia University
- Yihan Wang ([email protected]), UCLA
- Jinqi (Kathryn) Chen ([email protected]), CMU
The team acknowledges the financial and advisory support from Prof. Zico Kolter ([email protected]), Prof. Cho-Jui Hsieh ([email protected]), Prof. Suman Jana ([email protected]), Prof. Bo Li ([email protected]), and Prof. Xue Lin ([email protected]).
Our library is released under the BSD 3-Clause license. A copy of the license is included here.