Find max flow with minimum cost

Swift implementation of Edmonds-Karp min cost max flow algorithm using adjacency matrix. You can set all costs to 0 to get regular maximum flow. Complexity is about O(|V|^4 * MAX_EDGE_COST)

Example

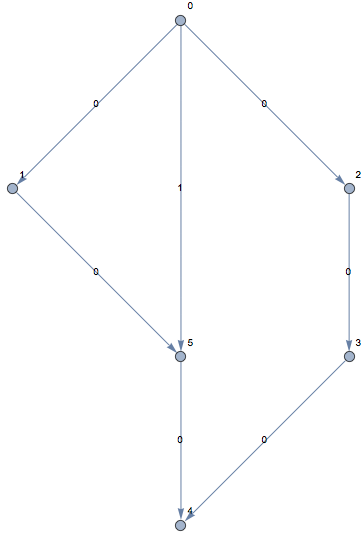
Assume we have graph as in image below

First, lets describe it using capacity matrix

// vertex count
let N = 6
var capacity = [[Int]](count: N, repeatedValue: [Int](count: N, repeatedValue: 0))

// connect edges with capacity 1
capacity[0][1] = 1
capacity[0][2] = 1
capacity[0][5] = 1
capacity[2][3] = 1
capacity[3][4] = 1
capacity[1][5] = 1
capacity[5][4] = 1

Next init cost matrix and make sure that we have one edge with higher cost (as in image above)

var cost = [[Int]](count: N, repeatedValue: [Int](count: N, repeatedValue: 0))
// add edge with higher cost
cost[0][5] = 1

Compute max flow and min cost values

let flow = MinCostMaxFlow()
let (totalFlow, totalCost) = flow.getMaxFlow(capacity, cost: cost, source: 0, sink: 4)
print("total flow: \(totalFlow), total cost: \(totalCost)")

will print: total flow: 2, total cost: 0