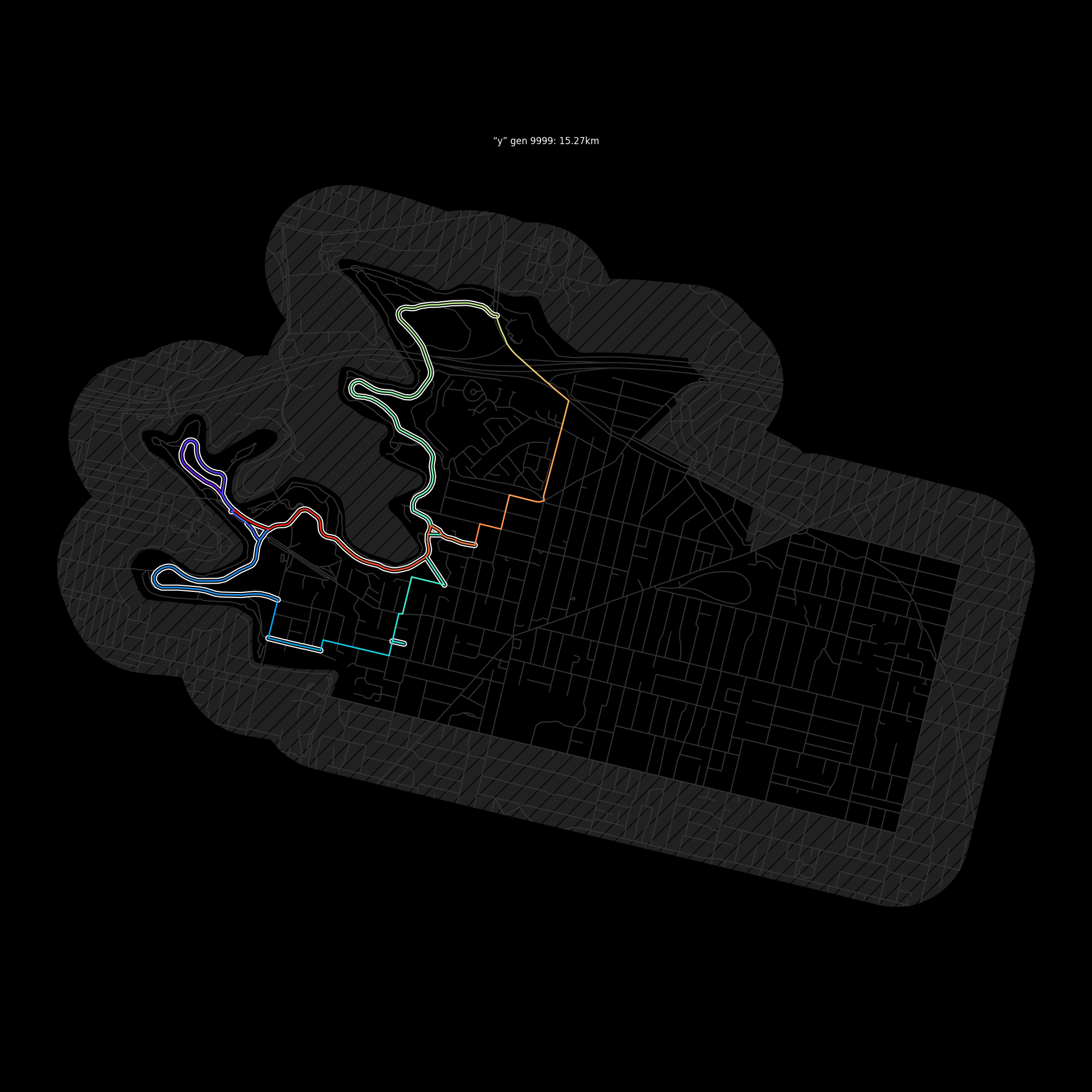
Melbourne, Australia had a savage 5km-radius lockdown for a few months in 2020. This knocked out my usual bike exercise routes. I started "burbing" my postcode and decided I needed to drag it out or I would quickly run out of streets. To do this, I rode only the streets beginning with A, then B, and so on.
I quickly got sick of finding all those streets on a map, then figuring out an efficient way to ride between them. The possibility that I had not used the best route haunted my dreams. So I got the computer to figure out the routes for me.
python route.py 3101 y -- -37.801506,145.0071469
No cached data for 3101. This will take a minute.
Reading postcode boundaries from ./postcodes-vic/ll_gda94/sde_shape/whole/VIC/VMADMIN/layer/postcode_polygon.shp
Reading roads from ./roads-vic/ll_gda2020/shape/whole_of_dataset/vic/VMTRANS/TR_ROAD.shp
Removing 0 goals because they are unreachable
Pre-solving 17 standins of 54 goal roads for 200 gens
200 12.45
Solving 54 goal roads for 10,000 generations. Ctrl-C to write best so far and quit.
2 21.97
3 20.93
4 20.26
6 19.09
11 18.69
19 17.79
32 16.26
51 15.84
271 15.84
1499 15.8
1996 15.27
10000 15.27python route.py <postcode> <letter> -- <home-coords><home-coords> is a lat,lon coordinate which you would like to start and
finish your ride at. I find the easiest way to get this is to find my house on
Google Maps and pull the coordinate from the URL.
To hit all the Q streets in Melbourne city starting at and returning to the GPO, you would use:
python route.py 3000 q -- -37.812990,144.962945
Clone and install the dependencies from dependencies.txt.
You then need to download the "TR_ROAD" dataset from data.vic.gov.au in ESRI Shapefile format. If you end up in the "spatial datamart" you are on the right track. If you only want to generate routes for a single postcode, you can download the dataset for just that postcode (though use a ~500m buffer) and it will work fine. You can also go right up to the whole of Victoria and that will work too.
This is a way bigger problem space than I expected. I thought that the difficult part would be wrangling map data and then performing route-finding across the map. But the real trick is figuring out in what order to visit your target roads. If you've got three targets roads (say Alpha street, Apple way and Acropolis close), there are twelve different ways to visit them: 3×2×1=6 combinations, then double it because you can visit each street in either direction. OK, twelve, that's not so bad is it? But this explodes out to ~7.2m combinations for only ten target roads.
And it gets worse. In the TR_ROAD dataset at least, roads are presented as short segments between intersections. That is, a long main road with ten intersections is not one single road, it's nine contiguous roads all with the same name. This is exactly what you want for routing, but it also makes that n-factorial explosion even worse. And you can't join the nine little roads together into one big road; sometimes the best route involves leaving the long road half way down and coming back to it later, which is not possible if you joined it up.
Rather than check every one of these combinations, this project uses a rough heuristic to find an initial route, then improves on it with a genetic algorithm.
Firstly the TR_ROAD dataset is loaded and cropped down to the target postcode. A small buffer is left around the boundary which leaves open the ability to route across concave parts of the postcode.
Within the postcode, the road data is built into a graph of edges between x,y coordinate vertices. I don't know if I can rely on every dataset to look like this, but TR_ROAD has identical coordinates for all roads terminating at an intersection which makes building the graph very easy. So, visually speaking, the graph is a bunch of straight lines between intersections describing where you can get from and to. And mathematically speaking, it's a graph.
The target roads are also picked out at this stage -- that is, every road starting with the letter Q, to use the earlier example. The target roads are then cleaned up. Contiguous roads are temporarily glued together and any with a total length too short are removed from the target list. Next, five of the targets are chosen at random as "witnesses"; any target which is unreachable from all five witnesses is assumed to be entirely unreachable and is also removed.
Then, a rough initial route is found by solving the problem at a lower resolution first. Contiguous target roads are temporarily glued together and from each contiguous bunch a single representative "stand-in" segment is picked. This cuts down the number of target roads by an order of magnitude (and therefore the problem space by 10-factorial). A route between the standins can be calculated fairly quickly. The initial solution is then found by ordering the target roads according to the order of their stand-ins. A solution takes the form of a list of target roads and which direction they should be traversed.
Finally, the most time-consuming step begins. A pool of solutions are generated from the initial solution by making random modifications to it. These are all scored according to their total length. The total length is determined by performing an A-star pathfind between each target road per their solution order and direction. The best three solutions are kept and the process repeated for a hardcoded 10,000 generations.
The solutions converge fairly quickly on a route within 5% of the optimal distance. The speed of convergence is very sensitive to how the random modifications are turned. Making adjacent swaps is too subtle, and making arbitrary swaps very unlikely to be an improvement. Remembering that generally the best route will involve traversing a contiguous series of road-segments from one end to the other rather than leaving it and returning to it, a very effective strategy is to randomise at the contiguous-series level, for example by swapping two contiguous series or by reversing a series. So these modifications are also made.