PyCopula is an easy-to-use Python library that allows you to study random variables dependencies with copulas. It comes with useful tools and features to plot, estimate or simulate on copulas.

• Online Documentation

Installation

Installation via pip always offers you the last stable version of the package.

pip install pycopula

However, if you are looking for latest updates, consider installation directly from sources.

git clone https://github.com/MaximeJumelle/pycopula.git
cd pycopula
python setup.py install

Features

PyCopula natively handle various families of copulas including :

• Archimean Copulas
  • Clayton
  • Gumbel
  • Joe
  • Frank
  • Ali-Mikhail-Haq
• Elliptic Copulas
  • Gaussian
  • Student

Estimation

Three methods of estimation, based on SciPy numerical optimization routines, are available to provide high flexibility during fitting process.

• Moments estimation on particular copulas
• Maximum Likelihood Estimation (MLE)
• Inference For Margins (IFM)
• Canonical Maximum Likelihood Estimation (CMLE)

Usage

PyCopula was designed to provide an easy-to-use interface that does not require a lot in both programming and computing. As a result, only a few lines are needed to properly fit any copulas, as demonstrated in the following code snippet.

import pandas as pd
from pycopula.copula import ArchimedeanCopula

data = pd.read_csv("data/classic.csv").values[:,1:]

archimedean = ArchimedeanCopula(family="gumbel", dim=2)
archimedean.fit(data, method="cmle")

Archimedean Copula (gumbel) :
*	Parameter : 1.605037

Visualization

3D PDF and CDF

Concentration Functions

Estimation

Simulation

Development

Currently, there are only a few features implemented in the library, which are the basics components for copula handling :

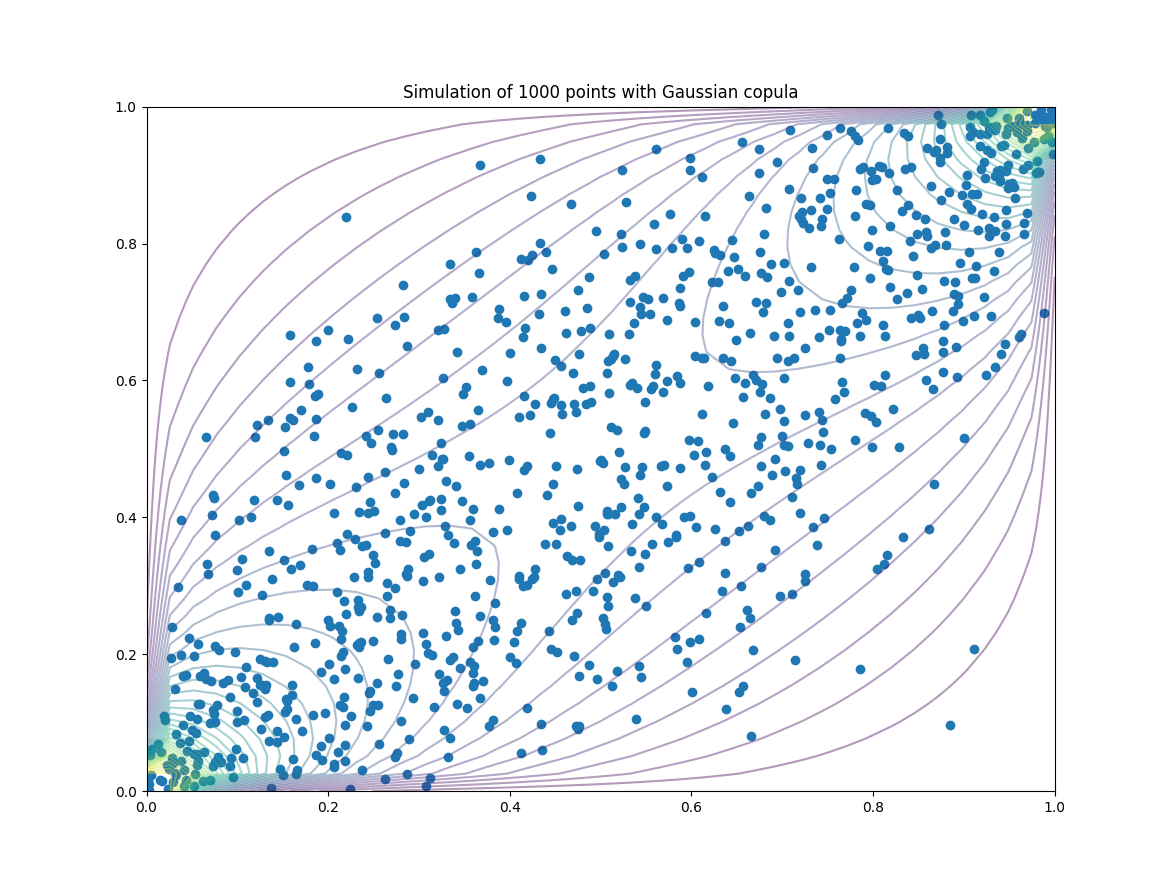
• Creating Archimedean, Gaussian and Student copulas
• 3D plot of PDF and CDF
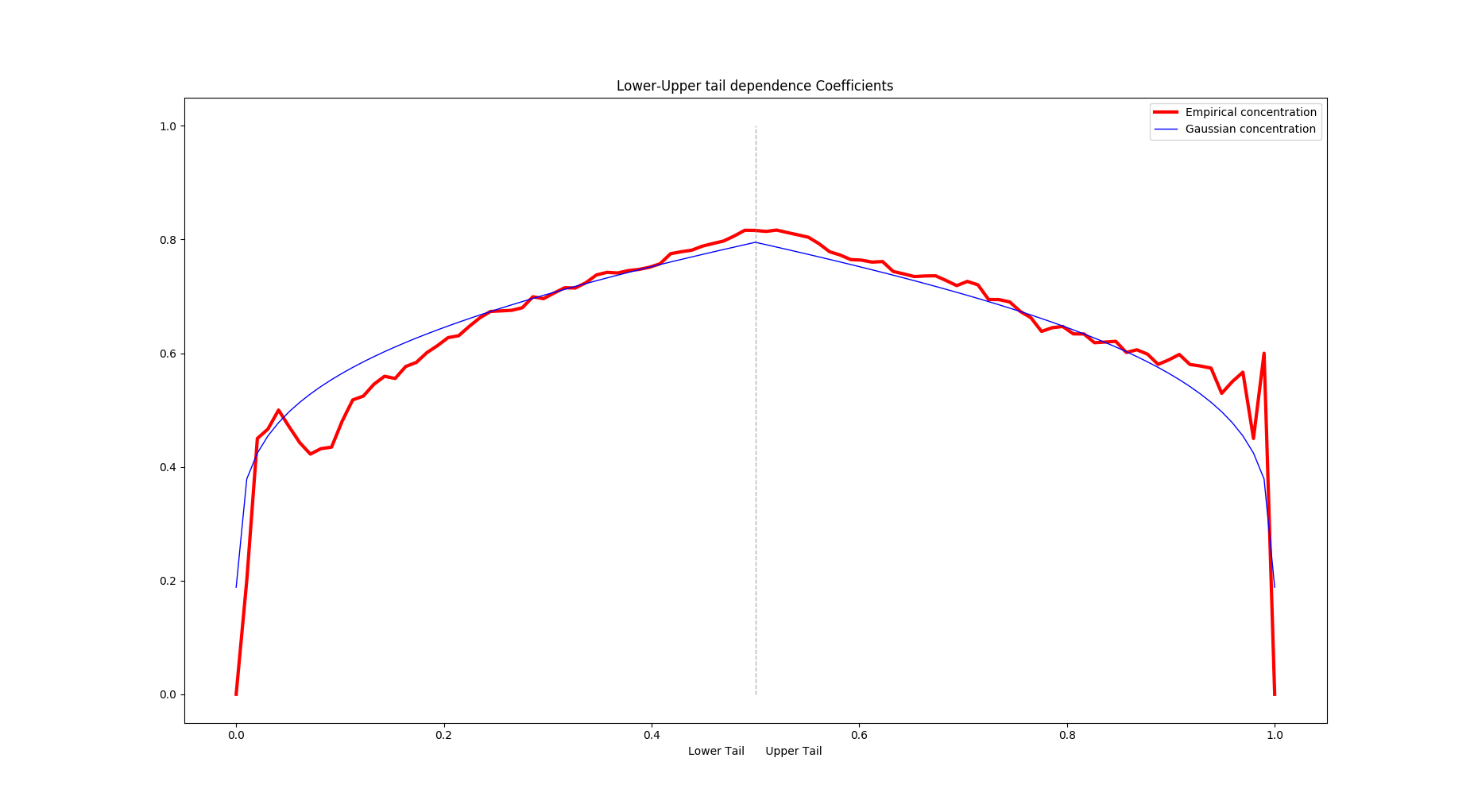
• Concentration functions and visualization
• Estimation of copulas parameters (CMLE, MLE, IFM)

In the future, I plan to release the following features :

• Goodness-of-fit
• Copula selection with criterions and statistical testing
• Examples of applications in real world with open data

Also, if you are interested in the project, I would be happy to collaborate with you since there are still quite a lot of improvements needed (computation, estimation methods, visualization) and that I don't have enough time on my hands to do it quickly.