seventrees

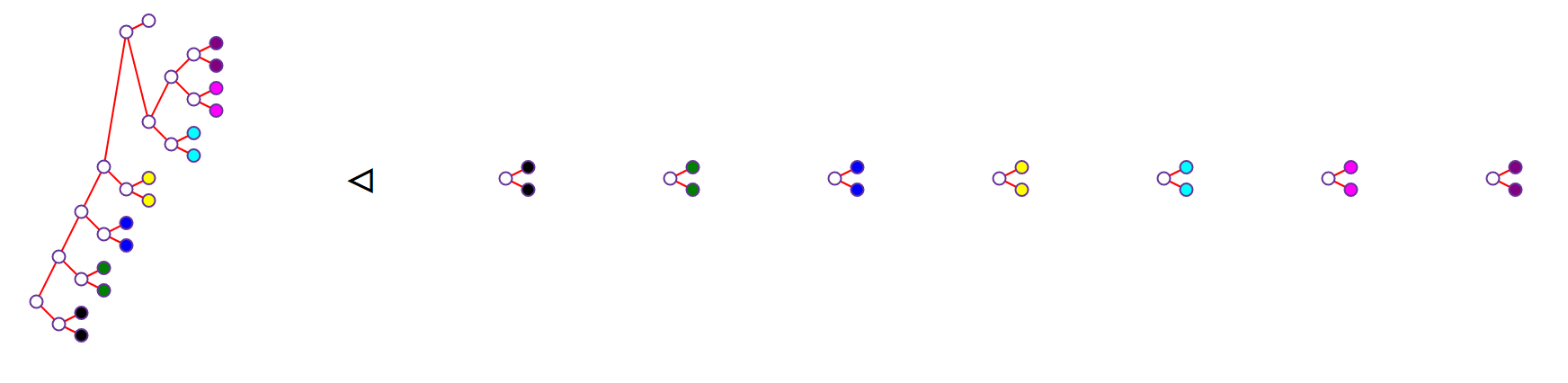
The datatype $T$ of trees is isomorphic to the type $T^7$ of seven-tuples of such trees! One can define two magical Haskell functions pack, unpack

data T = Leaf | Branch T T 

pack :: (T,T,T,T,T,T,T) -> T
unpack :: T -> (T,T,T,T,T,T,T)

which are inverses to each other and furthermore run in constant time. The procedure is essentially one giant, intricate pattern matching. It is not possible to take one tree apart like this into $n$ trees for any other $1 < n < 7$.

But how does the unpacking procedure actually look like? I've written an animation in Javascript to try it out interactively. I am also using colors to indicate some of the workings of the algorithm. You can try out the animation here.

Implementation

The cleanest way to explain the seven trees isomorphism is using the game of nuclear pennies. In the game, we can make a sequence of moves, called merge(n) or split(n), to move tokens around on a strip. We begin at position 1 (corresponding to one tree), and we win the game if we reach position 7 (seven trees).

Each move corresponds to a function call

function split(n, trees) {
   if (trees.length == (n+1)) {
       if (trees[n].isLeaf) {
           return trees.slice(0,n);
       } else {
           let tree = trees[n];
           return trees.slice(0,n).concat([tree.left, tree.right]);
       }
   } 
   else {
       return trees;
   }
}

which takes a list $t[0], ..., t[n]$ of n+1 trees and pattern maches on $t[n]$. If it is a leaf, we return a list of size n (dropping the leaf), if it is a branch, we return a list of size n+2. This operation is inverted by merge(n), that is assembling the list again. We can now write down the winning strategy of nuclear pennies in the program

// A winning strategy for nuclear pennies

let cmdsOneToSeven = [
    makeCommand('split',0),
    makeCommand('split',1),
    makeCommand('split',2),
    makeCommand('split',3),
    makeCommand('merge',0,{t:1}),
    makeCommand('merge',1,{tl:1}),
    makeCommand('split',4),
    makeCommand('merge',2),
    makeCommand('split',5),
    makeCommand('merge',1),
    makeCommand('split',4),
    makeCommand('merge',2),
    makeCommand('split',5,{tr:1}),
    makeCommand('split',6,{t:1}),
    makeCommand('merge',3),
    makeCommand('merge',4),
    makeCommand('merge',5),
    makeCommand('merge',6)
]

and translate this to the corresponding calls to split and merge. One small difficulty: At two points in the algorithms, there happen to be different ways a list of $n$ trees can arise (corresponding to having two pennies on the same position in the game). We need to keep these apart so we can process them correctly; we solve this by adding little tags to tree lists, and telling the functions on which tags they should operate (that's the optional l,lt,tr arguments). The tagged implementation of split and merge look like

function split(taggedtrees, n, t, tl, tr) {
    let [tag, trees] = taggedtrees;
    if (trees.length == (n+1) && tag === t) {
        if (trees[n].isLeaf) {
            return [ tl, trees.slice(0,n) ];
        } else {
            let tree = trees[n];
            return [ tr, trees.slice(0,n).concat([tree.left, tree.right]) ]
        }
    } 
    else {
        return taggedtrees;
    }
}

function merge(taggedtrees, n, t, tl, tr) {
    let [tag, trees]= taggedtrees;
    if (trees.length == (n+2) && tag == tr) {
        let l = trees[n];
        let r = trees[n+1];
        return [ t, trees.slice(0,n).concat([ branch(l,r) ]) ];     
    } 
    else if (trees.length == n && tag == tl) {
        return [ t, trees.concat([ leaf() ]) ];
    }
    else {
        return taggedtrees;
    }
}