-
Notifications
You must be signed in to change notification settings - Fork 62
Random stuff
Автор: Левицкий Илья
«Генерация случайных чисел слишком важна, чтобы оставлять её на волю случая» - Роберт Кавью
Здесь приведен короткой обзор простых методов генерации (псевдо)случайных чисел. Перечисленные подходы не считаются криптографически стойкими, но все же могут удовлетворить требования большинства программистов.
Случайные числа применимы во многих сферах: криптография, имитационное моделирование, протоколы передачи данных и, конечно, игры. Людям, практикующим микроконтроллеры, скорее всего интересны последние два направления. Постоянная генерация по-настоящему СЛУЧАЙНЫХ чисел это непростая задача. В качестве источников энтропии чаще всего берут различные источники шумов (звук, ток, ЭМ волны и т.д.) или радиации. Выбор качественного источника необходим для криптографических приложений, где истинная случайность важна. Но иногда случайность нужна «бытовая», чтобы человеку что-то казалось случайным, не подчиняющимся очевидному закону. В этом обзоре разбираются способы реализовать генераторы случайных чисел. Причём приведённые способы легки для написания, а сами генераторы требуют мало машинных ресурсов и генерируют достаточную на вид случайность.
Приницип ГПСЧ следующий: формируется последовательность из чисел, элементы которой почти независимы друг от друга, но в то же время каждый следующий элемент рассчитан с использованием предыдущих элементов (или прошлого состояния генератора). Такой подход позволяет воспроизвести этот ряд по так называемому зерну (seed), начальному элементу или состоянию. Это может быть важно например для отладки. Ещё один важный пункт: генераторы периодичны. Рано или поздно генератор вернётся к начальному состоянию и будет воспроизводить последовательность заново, так как в регистре бит конечного размера можно сохранить лишь конечное множество чисел. Поэтому при построении генератора важно, чтобы период этого повторения был по возможности большой. Рассмотрим примеры генераторов:
Считаем Следующий элемент последовательности Y считается на основе прошлого элемента X по следующей формуле:
Y = (а*Х+b) mod m
Расчёт нового элемента производится достаточно быстро. Последовательность фактически определяется 3 константами: a, b, m. Примеры «хороших» констант, дающих максимальный период, можно отыскать самостоятельно.
Возможно, у читателей возникнет сомнение насчёт скорости из-за операции «взятие числа по модулю m». Если взять m равное степени двойки, то эта операция просто сводится к побитовому И с некоторой маской. Только тогда для таких m надо учитывать, что младшие биты проявляют меньшую случайность чем старшие. По этой причине иногда одну половину числа просто отбрасывают.
Регистр сдвига с линейной обратной связью (РСЛОС, LFSR)
РСЛОС состоит из двух основных частей: самого сдвигового регистра и обратной связи. Следующий сгенерированный бит определяется как линейная комбинация, или просто битовая сумма, XOR, нескольких бит в определённых позициях самого регистра.
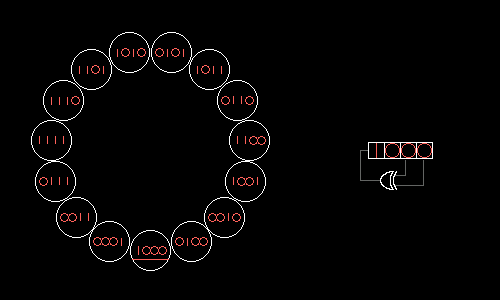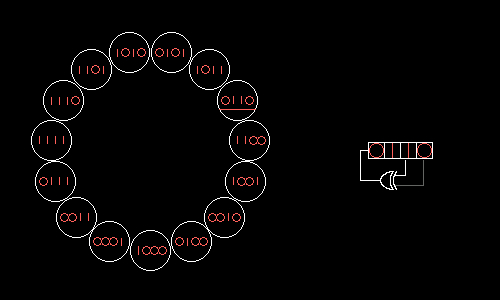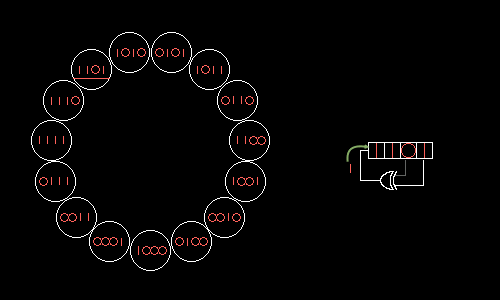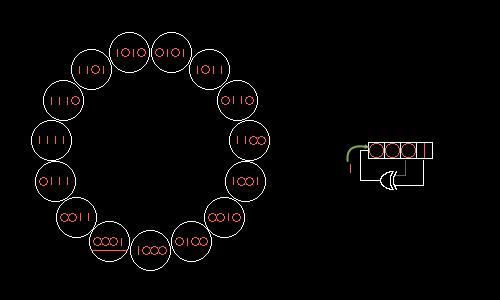
Рис. 1. Принцип работы РСЛОС (credits: Wikipedia)
Стоит заметить, что после одной итерации тут случайным является только один новый бит. Все остальные, очевидно, просто сдвинуты на 1. Поэтому каждый такт считать содержимое всего регистра случайным нельзя. Значения просто отличаются примерно в два раза. Если же снимать значения регистра через число итераций большее, чем размер самого регистра, то всё число уже можно использовать. Дополнительное удобство заключается в возможности самому выбрать длину регистра.
Вопросом остаётся только, от каких битов считать исключающее ИЛИ. Эти позиции можно определить по степеням генерирующих полиномов. Если взять генерирующий полином, то его самая большая степень укажет размер регистра. Если от каждой степени отнять по 1, то мы и получим нужные нам номера позиций, если считать от нуля. Во всех полиномах также присутствует единица, слагаемое нулевой степени. Единицу можно игнорировать. Если грубо, то она просто указывает на то, что чтобы получить следующее число нужно просуммировать указанные биты и полученный бит положить следующим в сдвиговый регистр. Формальное математическое обоснование построения и использования полиномов в этом обзоре не приводится. В качестве примера для 32-битного регистра можно просуммировать 31-й, 30-й, 29-й, 27-й, 25-й и 0-й биты. Полученный РСЛОС имеет максимальный период 232-1. Код для такого регистра на языке Си следующий:
int LFSR_Fibonacci (void)
{
static unsigned long S = 0x00000001;
S = ((((S >> 31) ^ (S >> 30) ^ (S >> 29) ^ (S >> 27) ^ (S >> 25) ^ S ) & 0x00000001 ) << 31 ) | (S >> 1);
return S & 0x00000001;
}Готовые позиции также можно найти здесь (Table of Low-Weight Binary Irreducible Polynomials, Gadiel Seroussi) или здесь (Efficient Shift Registers, LFSR Counters, and Long Pseudo- Random Sequence Generators, Xilinx, page 5). Обратите внимание, что в этих источниках нумерация от начинается единицы. А также иногда используется операция XNOR, а не XOR.
Кроме алгоритма Фибоначчи существует еще много других алгоритм, например, алгоритм Галуа.
Последовательность Фибоначчи известна многим. В последовательности каждое число является суммой двух предыдущих, за исключением первых двух элементов. Эта позаимствована для метод Фибоначчи. Только сложение производится по модулю 2m, m - четное. Было выяснено, что такая последовательность не очень случайна. Поэтому была предложена доработка:
Xn= (Xn-24 + Xn-55) mod 2m
Метод замечателен своей скоростью — одна операция на новое число. В качестве недостатка — необходимость хранить последние 55 чисел. А также первые элементы для инициализации необходимо записать заранее, или сгенерировать иначе. Кроме того, важно чтобы не все числа были чётные; в противном случае все элементы последовательности будут чётными.
24 и 55 - это запаздывания. Их подобрали специально так, чтобы младшие биты в этой последовательности имели самый большой период — 255-1. Существуют и другие комбинации, например 19 и 52.
На основе данного метода построены алгоритмы Mush, Fish или Pike. Они включают в себя два или три генератора Фибоначчи с запаздываниями. Их выходы складываются операцией XOR и результат является выходом самих алгоритмов. Особенность заключается в том, что вычисление следующего элемента последовательности происходит не на всех взятых генераторах сразу, а лишь на некоторых, в зависимости от битов переноса при сложении на каждом генераторе. Тот факт, что работают не всегда все генераторы, называется прореживанием (shrinking). Эти три алгоритма когда-то были предложены для использования в криптографии, однако сейчас для каждого уже найден способ взлома.
Пример плохой таблицы случайных чисел:
int gen_rand (void) {
return 4;
//picked by fair die toss
}Для должной эффективности таблицы обычно порядка тысяч или миллионов элементов. Их генерируют истинно случайно, заранее, записывают их в память, и потом используют. Например для генерации псевдослучайных чисел. Или же такая таблица может представлять из себя банк секретных ключей, который заранее сформировали одинаково для двух устройств, чтобы в дальнейшем можно было наладить между ними зашифрованную передачу данных.
У читателя могла появиться ещё одна мысль. Почему бы не брать в качестве источника случайностей внешние события, например, нажатие кнопок пользователем или точное время прибытия сообщения от другого устройства. И это действительно используется на практике. Такие случайные внешние события можно использовать в качестве зерна для псевдослучайных генераторов.
Ещё один последний пункт. В серии МК STM32F4 есть встроенная периферия TRNG. Это истинный генератор случайных чисел, реализованный, как аналоговый источник тока. В токе присутствует шум, охваченный обратной связью. Для получения самих 32-битных случайных чисел используют уже известным нам LFSR. Таким образом счастливые обладатели серии F4 могут сразу читать случайные числа из регистра.
"Как хороша ваша реакция?" Проверьте с помощью игры на выживание «Успей нажать!».
Суть игры такова: в случайный момент времени (в каком-то отрезке) загорается светодиод. Пока он горит нужно нажать на кнопку. Если игрок успел, то светодиод сразу тухнет, прибавляется очко. Если не успел, то снимается жизнь. После потери всех жизней игра заканчивается. С количеством успехов рационально растет сложность - длительность горения светодиода укорачивается. Количество очков (или сразу и количество жизней) можно выводить на индикатор. Спецэффекты при изменении очков/жизней (типа моргания) приветствуются. Игра перезапускается кнопкой RESET.