README.md

1706. 球会落何处

English Version

题目描述

用一个大小为 m x n 的二维网格 grid 表示一个箱子。你有 n 颗球。箱子的顶部和底部都是开着的。

箱子中的每个单元格都有一个对角线挡板，跨过单元格的两个角，可以将球导向左侧或者右侧。

• 将球导向右侧的挡板跨过左上角和右下角，在网格中用 1 表示。
• 将球导向左侧的挡板跨过右上角和左下角，在网格中用 -1 表示。

在箱子每一列的顶端各放一颗球。每颗球都可能卡在箱子里或从底部掉出来。如果球恰好卡在两块挡板之间的 "V" 形图案，或者被一块挡导向到箱子的任意一侧边上，就会卡住。

返回一个大小为 n 的数组 answer ，其中 answer[i] 是球放在顶部的第 i 列后从底部掉出来的那一列对应的下标，如果球卡在盒子里，则返回 -1 。

 

示例 1：

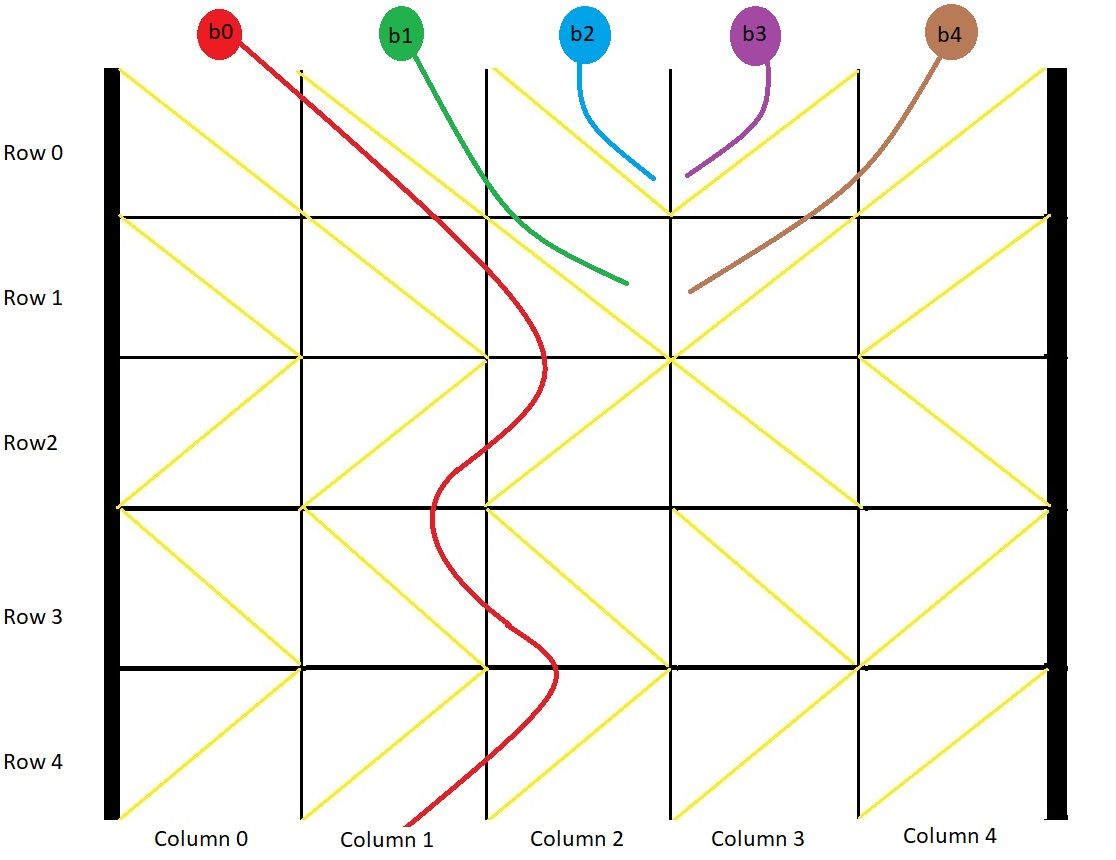
输入：grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
输出：[1,-1,-1,-1,-1]
解释：示例如图：
b0 球开始放在第 0 列上，最终从箱子底部第 1 列掉出。
b1 球开始放在第 1 列上，会卡在第 2、3 列和第 1 行之间的 "V" 形里。
b2 球开始放在第 2 列上，会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b3 球开始放在第 3 列上，会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b4 球开始放在第 4 列上，会卡在第 2、3 列和第 1 行之间的 "V" 形里。

示例 2：

输入：grid = [[-1]]
输出：[-1]
解释：球被卡在箱子左侧边上。

示例 3：

输入：grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]
输出：[0,1,2,3,4,-1]

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• grid[i][j] 为 1 或 -1

解法

球被卡住共有 4 种情况：

1. 球位于最左一列，并且球所在的单元格单元格挡板将球导向左侧
2. 球位于最右一列，并且此单元格挡板将球导向右侧
3. 球所在的单元格挡板将球导向右侧，并且球右侧相邻单元格挡板将球导向左侧
4. 球所在的单元格挡板将球导向左侧，并且球左侧相邻单元格挡板将球导向右侧

DFS 搜索即可。

Python3

class Solution:
    def findBall(self, grid: List[List[int]]) -> List[int]:
        m, n = len(grid), len(grid[0])

        def dfs(i, j):
            nonlocal m, n
            if i == m:
                return j
            if j == 0 and grid[i][j] == -1:
                return -1
            if j == n - 1 and grid[i][j] == 1:
                return -1
            if grid[i][j] == 1 and grid[i][j + 1] == -1:
                return -1
            if grid[i][j] == -1 and grid[i][j - 1] == 1:
                return -1
            return dfs(i + 1, j + 1) if grid[i][j] == 1 else dfs(i + 1, j - 1)

        return [dfs(0, j) for j in range(n)]

Java

class Solution {
    private int m;
    private int n;
    private int[][] grid;

    public int[] findBall(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        int[] ans = new int[n];
        for (int j = 0; j < n; ++j) {
            ans[j] = dfs(0, j);
        }
        return ans;
    }

    private int dfs(int i, int j) {
        if (i == m) {
            return j;
        }
        if (j == 0 && grid[i][j] == -1) {
            return -1;
        }
        if (j == n - 1 && grid[i][j] == 1) {
            return -1;
        }
        if (grid[i][j] == 1 && grid[i][j + 1] == -1) {
            return -1;
        }
        if (grid[i][j] == -1 && grid[i][j - 1] == 1) {
            return -1;
        }
        return grid[i][j] == 1 ? dfs(i + 1, j + 1) : dfs(i + 1, j - 1);
    }
}

C++

class Solution {
public:
    int m, n;
    vector<vector<int>> grid;

    vector<int> findBall(vector<vector<int>>& grid) {
        this->grid = grid;
        m = grid.size();
        n = grid[0].size();
        vector<int> ans(n);
        for (int j = 0; j < n; ++j) ans[j] = dfs(0, j);
        return ans;
    }

    int dfs(int i, int j) {
        if (i == m) return j;
        if (j == 0 && grid[i][j] == -1) return -1;
        if (j == n - 1 && grid[i][j] == 1)  return -1;
        if (grid[i][j] == 1 && grid[i][j + 1] == -1) return -1;
        if (grid[i][j] == -1 && grid[i][j - 1] == 1) return -1;
        return grid[i][j] == 1 ? dfs(i + 1, j + 1) : dfs(i + 1, j - 1);
    }
};

Go

func findBall(grid [][]int) []int {
	m, n := len(grid), len(grid[0])

	var dfs func(i, j int) int
	dfs = func(i, j int) int {
		if i == m {
			return j
		}
		if j == 0 && grid[i][j] == -1 {
			return -1
		}
		if j == n-1 && grid[i][j] == 1 {
			return -1
		}
		if grid[i][j] == 1 && grid[i][j+1] == -1 {
			return -1
		}
		if grid[i][j] == -1 && grid[i][j-1] == 1 {
			return -1
		}
		if grid[i][j] == 1 {
			return dfs(i+1, j+1)
		}
		return dfs(i+1, j-1)
	}

	var ans []int
	for j := 0; j < n; j++ {
		ans = append(ans, dfs(0, j))
	}
	return ans
}

...