README_EN.md

1706. Where Will the Ball Fall

中文文档

Description

You have a 2-D grid of size m x n representing a box, and you have n balls. The box is open on the top and bottom sides.

Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.

• A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as 1.
• A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as -1.

We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V" shaped pattern between two boards or if a board redirects the ball into either wall of the box.

Return an array answer of size n where answer[i] is the column that the ball falls out of at the bottom after dropping the ball from the ith column at the top, or -1 if the ball gets stuck in the box.

 

Example 1:

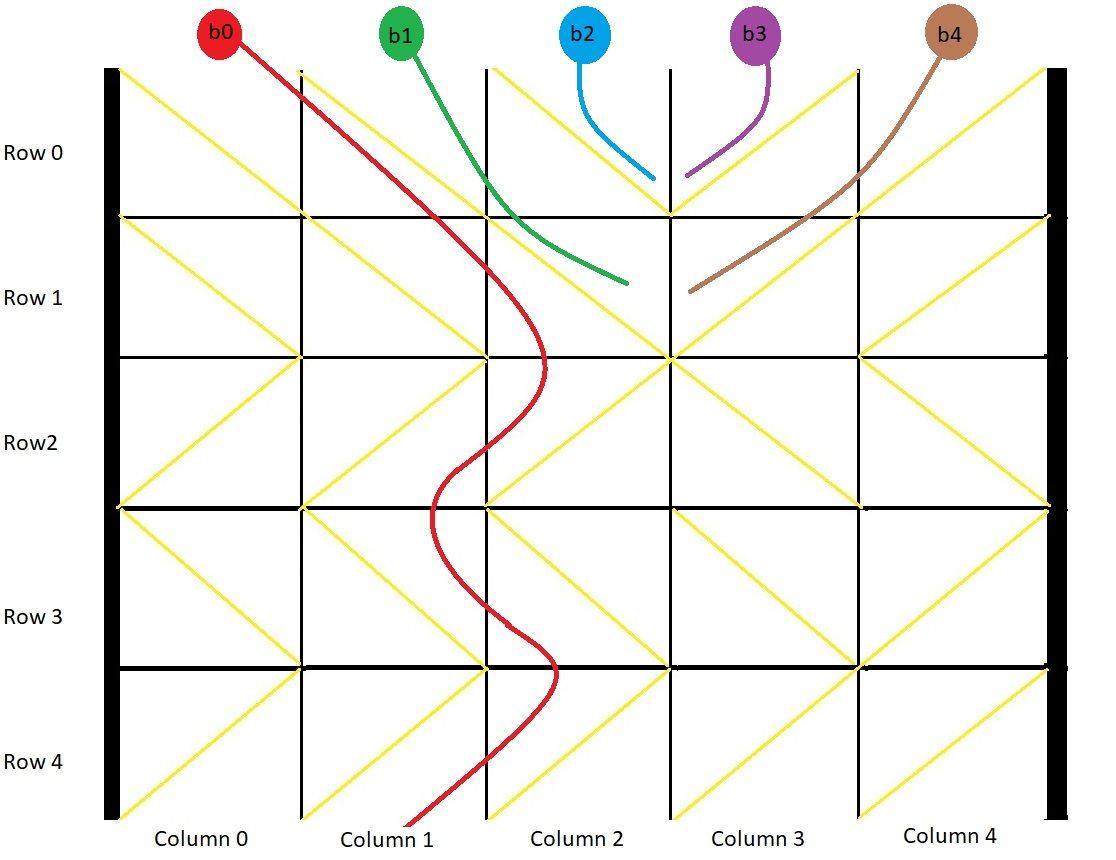
Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
Output: [1,-1,-1,-1,-1]
Explanation: This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.

Example 2:

Input: grid = [[-1]]
Output: [-1]
Explanation: The ball gets stuck against the left wall.

Example 3:

Input: grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]
Output: [0,1,2,3,4,-1]

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• grid[i][j] is 1 or -1.

Solutions

Python3

class Solution:
    def findBall(self, grid: List[List[int]]) -> List[int]:
        m, n = len(grid), len(grid[0])

        def dfs(i, j):
            nonlocal m, n
            if i == m:
                return j
            if j == 0 and grid[i][j] == -1:
                return -1
            if j == n - 1 and grid[i][j] == 1:
                return -1
            if grid[i][j] == 1 and grid[i][j + 1] == -1:
                return -1
            if grid[i][j] == -1 and grid[i][j - 1] == 1:
                return -1
            return dfs(i + 1, j + 1) if grid[i][j] == 1 else dfs(i + 1, j - 1)

        return [dfs(0, j) for j in range(n)]

Java

class Solution {
    private int m;
    private int n;
    private int[][] grid;

    public int[] findBall(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        int[] ans = new int[n];
        for (int j = 0; j < n; ++j) {
            ans[j] = dfs(0, j);
        }
        return ans;
    }

    private int dfs(int i, int j) {
        if (i == m) {
            return j;
        }
        if (j == 0 && grid[i][j] == -1) {
            return -1;
        }
        if (j == n - 1 && grid[i][j] == 1) {
            return -1;
        }
        if (grid[i][j] == 1 && grid[i][j + 1] == -1) {
            return -1;
        }
        if (grid[i][j] == -1 && grid[i][j - 1] == 1) {
            return -1;
        }
        return grid[i][j] == 1 ? dfs(i + 1, j + 1) : dfs(i + 1, j - 1);
    }
}

C++

class Solution {
public:
    int m, n;
    vector<vector<int>> grid;

    vector<int> findBall(vector<vector<int>>& grid) {
        this->grid = grid;
        m = grid.size();
        n = grid[0].size();
        vector<int> ans(n);
        for (int j = 0; j < n; ++j) ans[j] = dfs(0, j);
        return ans;
    }

    int dfs(int i, int j) {
        if (i == m) return j;
        if (j == 0 && grid[i][j] == -1) return -1;
        if (j == n - 1 && grid[i][j] == 1)  return -1;
        if (grid[i][j] == 1 && grid[i][j + 1] == -1) return -1;
        if (grid[i][j] == -1 && grid[i][j - 1] == 1) return -1;
        return grid[i][j] == 1 ? dfs(i + 1, j + 1) : dfs(i + 1, j - 1);
    }
};

Go

func findBall(grid [][]int) []int {
	m, n := len(grid), len(grid[0])

	var dfs func(i, j int) int
	dfs = func(i, j int) int {
		if i == m {
			return j
		}
		if j == 0 && grid[i][j] == -1 {
			return -1
		}
		if j == n-1 && grid[i][j] == 1 {
			return -1
		}
		if grid[i][j] == 1 && grid[i][j+1] == -1 {
			return -1
		}
		if grid[i][j] == -1 && grid[i][j-1] == 1 {
			return -1
		}
		if grid[i][j] == 1 {
			return dfs(i+1, j+1)
		}
		return dfs(i+1, j-1)
	}

	var ans []int
	for j := 0; j < n; j++ {
		ans = append(ans, dfs(0, j))
	}
	return ans
}

...