Object composition. In particular: Link functions up into callable objects (e.g. pipelines, DAGs, etc.)
To install: pip install meshed
Note: The initial focuus of meshed was on DAGs, a versatile and probably most known kind of composition of functions,
but meshed aims at capturing much more than that.
from meshed import DAG
def this(a, b=1):
return a + b
def that(x, b=1):
return x * b
def combine(this, that):
return (this, that)
dag = DAG((this, that, combine))
print(dag.synopsis_string())x,b -> that_ -> that
a,b -> this_ -> this
this,that -> combine_ -> combine
But what does it do?
It's a callable, with a signature:
from inspect import signature
signature(dag)<Signature (x, a, b=1)>
And when you call it, it executes the dag from the root values you give it and returns the leaf output values.
dag(1, 2, 3) # (a+b,x*b) == (2+3,1*3) == (5, 3)(5, 3)
dag(1, 2) # (a+b,x*b) == (2+1,1*1) == (3, 1)(3, 1)
You can see (and save image, or ascii art) the dag:
dag.dot_digraph()You can extend a dag
dag2 = DAG([*dag, lambda this, a: this + a])
dag2.dot_digraph()You can get a sub-dag by specifying desired input(s) and outputs.
dag2[['that', 'this'], 'combine'].dot_digraph()The above DAG was created straight from the functions, using only the names of the functions and their parameters to define how to hook the network up.
But if you didn't write those functions specifically for that purpose, or you want to use someone else's functions, one would need to specify the relation between parameters, inputs and outputs.
For that purpose, functions can be adapted using the class FuncNode. The class allows you to essentially rename each of the parameters and also specify which output should be used as an argument for any other functions.
Let us consider the example below.
def f(a, b):
return a + b
def g(a_plus_b, d):
return a_plus_b * dSay we want the output of f to become the value of the parameter a_plus_b. We can do that by assigning the string 'a_plus_b' to the out parameter of a FuncNode representing the function f:
f_node = FuncNode(func=f, out="a_plus_b")We can now create a dag using our f_node instead of f:
dag = DAG((f_node, g))Our dag behaves as wanted:
dag(a=1, b=2, d=3)
9Now say we would also like for the value given to b to be also given to d. We can achieve that by binding d to b in the bind parameter of a FuncNode representing g:
g_node = FuncNode(func=g, bind={"d": "b"})The dag created with f_node and g_node has only two parameters, namely a and b:
dag = DAG((f_node, g_node))
dag(a=1, b=2)
6dag[input_nodes:output_nodes] is the sub-dag made of intersection of all
descendants of input_nodes
(inclusive) and ancestors of output_nodes (inclusive), where additionally,
when a func node is contained, it takes with it the input and output nodes
it needs.
from meshed import DAG
def f(a): ...
def g(f): ...
def h(g): ...
def i(h): ...
dag = DAG([f, g, h, i])
dag.dot_digraph()Get a subdag from g_ (indicates the function here) to the end of dag
subdag = dag['g_',:]
subdag.dot_digraph()From the beginning to h_
dag[:, 'h_'].dot_digraph()From g_ to h_ (both inclusive)
dag['g_', 'h_'].dot_digraph()Above we used function (node names) to specify what we wanted, but we can also use names of input/output var-nodes. Do note the difference though. The nodes you specify to get a sub-dag are INCLUSIVE, but when you specify function nodes, you also get the input and output nodes of these functions.
The dag['g_', 'h_'] give us a sub-dag starting at f (the input node),
but when we ask dag['g', 'h_'] instead, g being the output node of
function node g_, we only get g -> h_ -> h:
dag['g', 'h'].dot_digraph()If we wanted to include f we'd have to specify it:
dag['f', 'h'].dot_digraph()Those were for simple pipelines, but let's now look at a more complex dag.
Note the definition: dag[input_nodes:output_nodes] is the sub-dag made of intersection of all
descendants of input_nodes
(inclusive) and ancestors of output_nodes (inclusive), where additionally,
when a func node is contained, it takes with it the input and output nodes
it needs.
We'll let the following examples self-comment:
from meshed import DAG
def f(u, v): ...
def g(f): ...
def h(f, w): ...
def i(g, h): ...
def j(h, x): ...
def k(i): ...
def l(i, j): ...
dag = DAG([f, g, h, i, j, k, l])
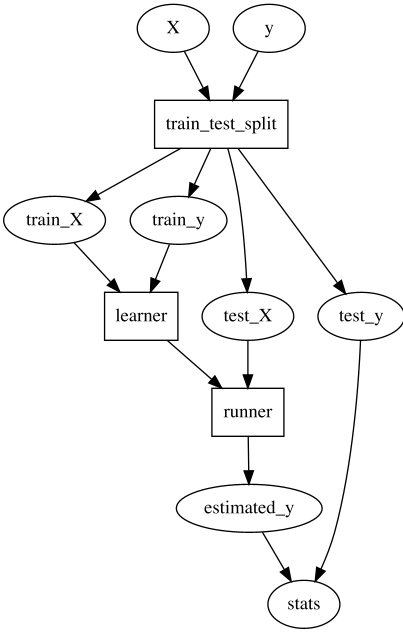
dag.dot_digraph()dag[['u', 'f'], 'h'].dot_digraph()dag['u', 'h'].dot_digraph()dag[['u', 'f'], ['h', 'g']].dot_digraph()dag[['x', 'g'], 'k'].dot_digraph()dag[['x', 'g'], ['l', 'k']].dot_digraph()Consider a simple train/test ML pipeline that looks like this.
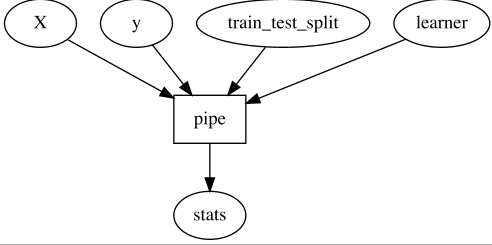
With this, we might decide we want to give the user control over how to do
train_test_split and learner, so we offer this interface to the user:
With that, the user can just bring its own train_test_split and learner
functions, and as long as it satisfied the
expected (and even better; declared and validatable) protocol, things will work.
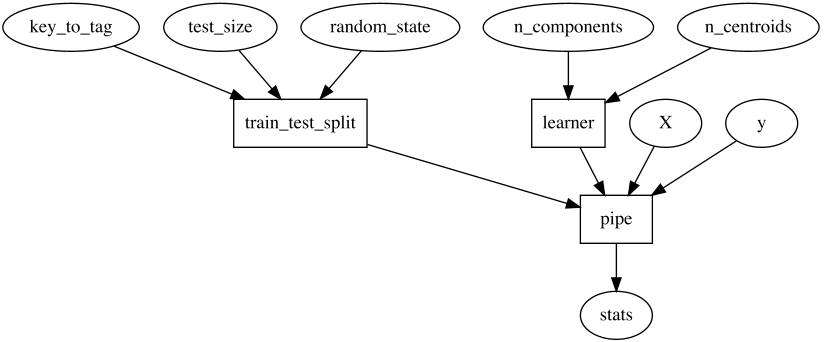
In some situations we'd like to fix some of how train_test_split and
learner work, allowing the user to control only some aspects of them.
This function would look like this:
And inside, it does:
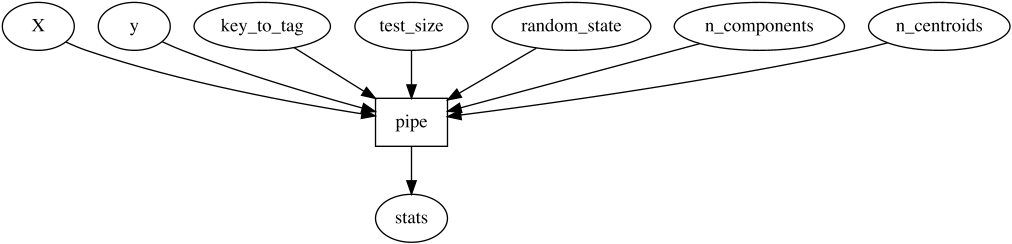
meshed allows us to easily manipulate such functional structures to
adapt them to our needs.
Tools that enable operations on graphs where graphs are represented by an adjacency Mapping.
Again.
Graphs: You know them. Networks. Nodes and edges, and the ecosystem descriptive or transformative functions surrounding these. Few languages have builtin support for the graph data structure, but all have their libraries to compensate.
The one you're looking at focuses on the representation of a graph as Mapping encoding
its adjacency list.
That is, a dictionary-like interface that specifies the graph by specifying for each node
what nodes it's adjacent to:
assert graph[source_node] == set_of_nodes_that_source_node_has_edges_toWe emphasize that there is no specific graph instance that you need to squeeze your graph into to
be able to use the functions of meshed. Suffices that your graph's structure is expressed by
that dict-like interface
-- which grown-ups call Mapping (see the collections.abc or typing standard libs for more information).
You'll find a lot of Mappings around pythons.
And if the object you want to work with doesn't have that interface,
you can easily create one using one of the many tools of py2store meant exactly for that purpose.
>>> from meshed.itools import edges, nodes, isolated_nodes
>>> graph = dict(a='c', b='ce', c='abde', d='c', e=['c', 'b'], f={})
>>> sorted(edges(graph))
[('a', 'c'), ('b', 'c'), ('b', 'e'), ('c', 'a'), ('c', 'b'), ('c', 'd'), ('c', 'e'), ('d', 'c'), ('e', 'b'), ('e', 'c')]
>>> sorted(nodes(graph))
['a', 'b', 'c', 'd', 'e', 'f']
>>> set(isolated_nodes(graph))
{'f'}
>>>
>>> from meshed.makers import edge_reversed_graph
>>> g = dict(a='c', b='cd', c='abd', e='')
>>> assert edge_reversed_graph(g) == {'c': ['a', 'b'], 'd': ['b', 'c'], 'a': ['c'], 'b': ['c'], 'e': []}
>>> reverse_g_with_sets = edge_reversed_graph(g, set, set.add)
>>> assert reverse_g_with_sets == {'c': {'a', 'b'}, 'd': {'b', 'c'}, 'a': {'c'}, 'b': {'c'}, 'e': set([])}