Diffeopt: optimisation on diffeomorphisms

Optimisation on diffeomorphisms using Pytorch to compute the gradient automatically.

The general idea is to be able to minimise expressions of the form $g ↦ F(g · x_0)$, where

• $g$ is a group element, typically a diffeomorphism
• $x_0$ is a template, typically either a density or a function (i.e., an image)
• $F$ is a cost function
• $g · x$ is an action (or representation) of the diffeomorphism group on densities or functions

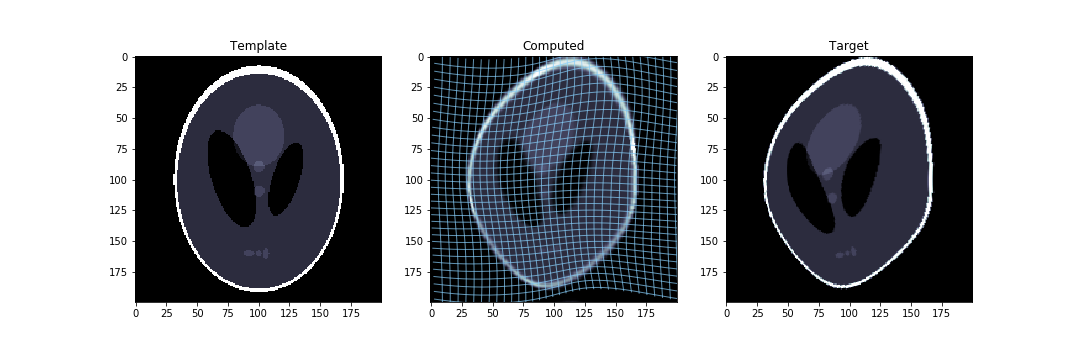
This can be used to do direct matching or indirect matching, both with several kinds of regularisation.

Check out this example notebook which illustrates the two kinds of matching.

Direct Matching with Orbit Minimisation

Suppose that we have a template I0 that we will use for the matching. It should be a pytorch tensor.

We need a notion of a group:

from diffeopt.group.ddmatch.group import DiffeoGroup
group = DiffeoGroup(I0.shape)

First, prepare the “network”, with one layer, which keeps a group element as a parameter, and computes one or several action on images. Here, we want to compute, for the same group element, an action on function and one on densities:

from diffeopt.group.ddmatch.representation import DensityRepresentation, FunctionRepresentation
from diffeopt.sum_representation import OrbitProblem
srep = OrbitProblem(FunctionRepresentation(group), DensityRepresentation(group))

Now we prepare an optimizer. It needs a learning rate and a cometric, as well as the network's parameters to be initialized:

from diffeopt.cometric.laplace import get_laplace_cometric
from diffeopt.optim import GroupOptimizer
go = GroupOptimizer(srep.parameters(), lr=1e-1, cometric=get_laplace_cometric(group, s=2))

We now prepare the necessary variables to compute the loss function.

from torch.nn import MSELoss
mse = MSELoss()
from diffeopt.utils import get_volume
vol = torch.ones(group.shape, dtype=torch.float64)/get_volume(group.shape)

The optimising loop is then as follows. Note that the loss function can be anything you like. Here, for direct matching, it depends on a target image I1.

for i in range(2**9):
    go.zero_grad()
    # forward pass
    I_, vol_ = srep(I0, vol)
    # the following loss function can be anything you like
    loss = mse(I_, I1) + mse(vol_, vol)
    if not i % 2**6:
        print(i, loss)
    # compute momenta
    loss.backward()
    # update the group element
    go.step()