billiards

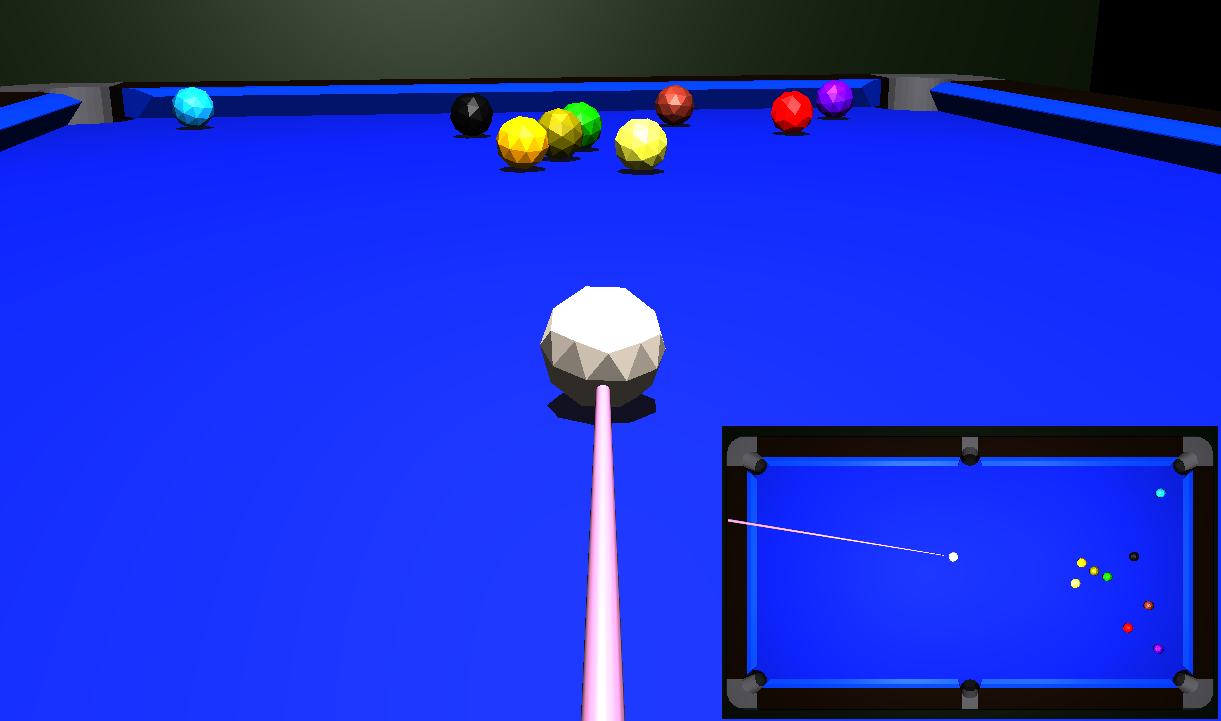
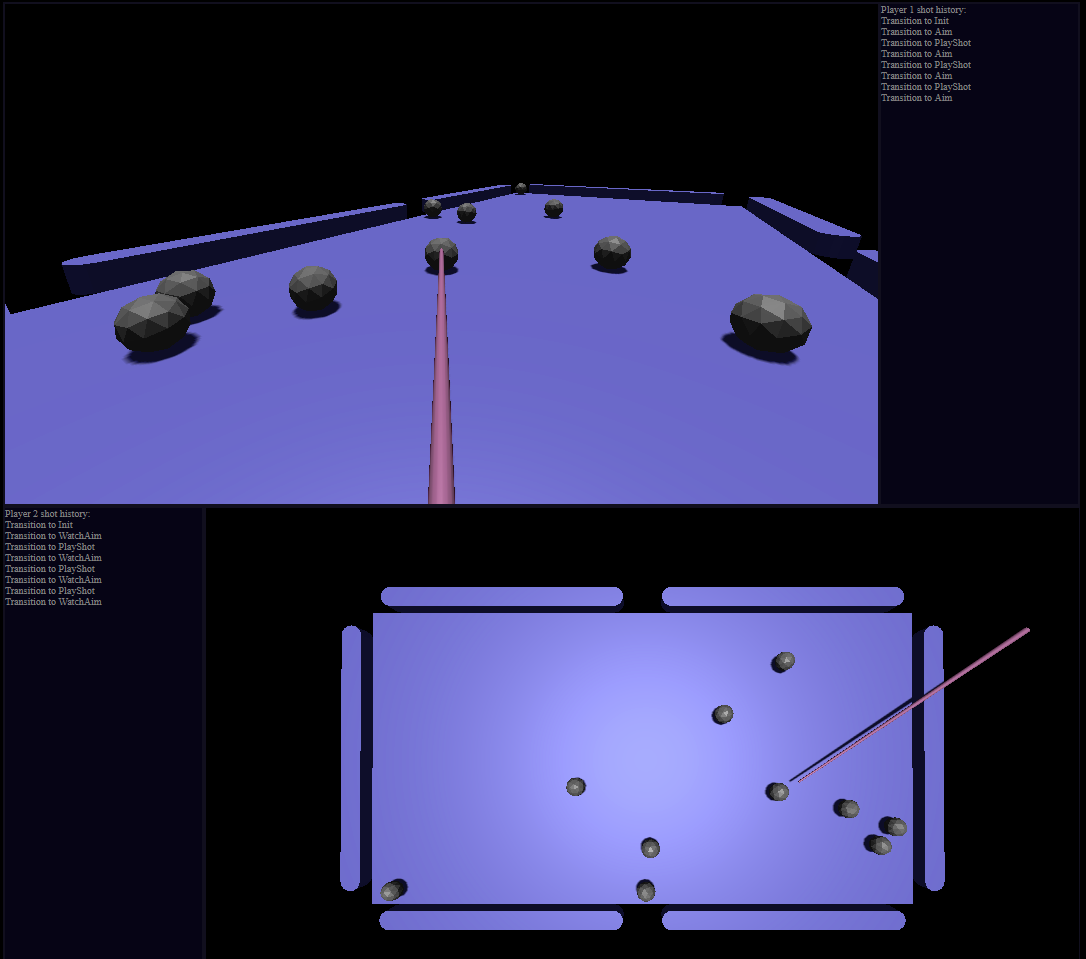
This is an open-source project bringing unsophisticated billiards physics written in typescript to the browser. Play pool, snooker, or 3-cushion online right here.

Features

• Backspin and sidespin well modeled.
• Presentation using WebGL in any modern browser on mobile, linux, mac or windows.
• Record and playback breaks.
• Two player online mode with node websocket server.
• Nine ball, Snooker and three cushion billiards rules.
• Deploys to github pages, vercel.com and render.com with github actions.

Online Demo

Demos run in all major desktop and mobile browsers and uses WebGL

• Nine ball ⬀ make a break and share replay link with friends
• Three cushion billiards ⬀ the ultimate test of physics and player (average on both counts)
• Snooker ⬀ we await the first 147 submission to the leaderboard.
• 4-ball Straight pool ⬀.
• Inspect physics and tweak constants using diagrams.
• Try to get on the leaderboard of highest breaks hosted on vercel.com
• Try two player online hosted on render.com

Reference material

• Papers on ball mechanics Han 2005 with important corrections by Kiefl.
• cushions, max spin, simulation and constants 1 2 3 4 5
• 3D graphics uses three.js
• Inline LaTeX editor for equations in README.md

Key equations

Based on Han 2005 paper

surface velocity

sliding motion

rolling motion

where

,

cushion bounce

This is based on a paper by Mathaven. Many of the figures from the paper are recreated to confirm correctness.

Slip velocity at cushion contact point I

$$ ẋ_I = \dot{v_x} + \dot{\omega_y} R \sin \theta - \dot{\omega_z} R \cos \theta \qquad ẏ'_I = -\dot{v_y} \sin \theta + \dot{\omega_x} R $$

$$ \phi = \arctan\left(\frac{ẏ'_I}{ẋ_I}\right) \qquad s = \sqrt{(ẋ_I)^2 + (ẏ'_I)^2} $$

Slip velocity at table contact point C

$$ ẋ_C = \dot{v_x} - \dot{\omega_y} R \qquad ẏ_C = \dot{v_y} + \dot{\omega_x} R $$

$$ \phi' = \arctan\left(\frac{ẏ'_I}{ẋ_I}\right) \qquad s' = \sqrt{(ẋ_C)^2 + (ẏ_C)^2} $$

Numerical solutions for the centroid velocity of the ball during compression and resititution phases.

$$ (\dot{v_x})_{n+1} - (\dot{v_x})_n = - \frac{1}{M} \left[\mu_w \cos(\phi) + \mu_s \cos(\phi') \cdot (\sin \theta + \mu_w \sin(\phi) \cos \theta)\right] \Delta P_I $$

$$ (\dot{v_y})_{n+1} - (\dot{v_y})_n = - \frac{1}{M} \left[ \cos \theta - \mu_w \sin \theta \sin \phi + \mu_s \sin \phi' \cdot \left( \sin \theta + \mu_w \sin \phi \cos \theta \right) \right] \Delta P_I $$

Numerical solutions for angular velocity of ball

$$ (\dot{\omega_x})_{n+1}−(\dot{\omega_x})_n = -\frac{5}{2MR}[\mu_w \sin(\phi) + \mu_s \sin(\phi') \times (\sin(\theta) + \mu_w \sin(\phi)\cos(\theta))]\Delta P_I $$

$$ (\dot{\omega_y})_{n+1}−(\dot{\omega_y})_n = -\frac{5}{2MR}[\mu_w \cos(\phi)\sin(\theta) - \mu_s \cos(\phi') \times (\sin(\theta) + \mu_w \sin(\phi)\cos(\theta))]\Delta P_I $$

$$ (\dot{\omega_z})_{n+1}−(\dot{\omega_z})_n = \frac{5}{2MR}(\mu_w \cos(\phi)\cos(\theta))\Delta P_I $$

$\theta$ is a constant of the angle of cushion contact above ball centre with $\sin(\theta) = 2/5$. $μ_s$ is the coefficient of sliding friction between the ball and table surface. $μ_w$ is the coefficient of sliding friction between the ball and the cushion.

Work done by the normal force at contact point $I$ along the $Z'$-axis which is aligned from the ball centre to I

$$ W_{Z'}^I(P_I^{(n+1)}) = W_{Z'}^I(P_I^{(n)}) + \frac{\Delta P_I}{2} \left( z'_I(P_I^{(n+1)}) + z'_I(P_I^{(n)}) \right) $$

The ball is assumed to be bouncing in the +y cushion. Compression phase iterates until

$$ \dot{v_y} <= 0 $$

For the restitution phase the iteration continues until the work done is

$$ W_{Z'}^I >= (1 - e_e^2) W_{compression} $$

Some of the Mathaven equations not supplied by the paper were inferred by LLMs and the code for them was initially generated by a combination of Claude, Qwen and GPT-4o.

Useful commands

Install

nvm use v18.17.1
yarn install
yarn dev
yarn gltfpack

This generates artefacts in /dist for prod deployment (e.g. on github static pages)

Run

yarn serve

Then open http://localhost:8080/ in your browser to play

Test

yarn test
yarn coverage

Maintain

yarn deps
yarn upgrade -L
yarn prettify

Two player

yarn websocket

the client uses query parameter ?websocketserver=wss://some-host to locate a websocket server, open http://localhost:8888/dist/multi.html to see options

Controls

Use mouse, touch screen or keyboard:

⇦ ⇨ Aim

Control ⇦ ⇨ Fine aim

⇧ ⇩ Topspin and backspin

Shift ⇦ ⇨ Side spin

Space Hit - hold for more power

Progress snapshots

July 2018

July 2019

March 2021

August 2023 (mobile)

top	aim

Star History

Licence

This project is open source and licensed under the GNU General Public License - see the LICENSE file for details. Contributions welcome.