# 概念
二叉树是树的一种, 由一个根结点和两棵互不相交的、分别称作左子树和右子树的二叉树组成, 每个结点最多有两个子节点.
# 二叉树的基本特征
每个结点最多有两个子结点
二叉树是有序树, 左子树和右子树不能颠倒次序, 即使树中某个结点只有一棵子树, 也要区别是左子树还是右子树.
# 递归性质
二叉树也是递归定义的, 二叉树中的子树还是二叉树.
二叉树的基本形态有5种:
- 空二叉树
- 仅有根结点的二叉树
- 仅有一棵左子树的二叉树
- 仅有一棵右子树的二叉树
- 有两棵子树的二叉树
根据二叉树中子结点的排布, 可将二叉树分为 非完全二叉树、完全二叉树、满二叉树、斜树
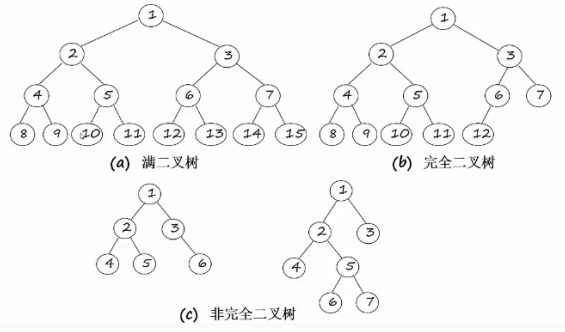
非完全二叉树就是普通的二叉树
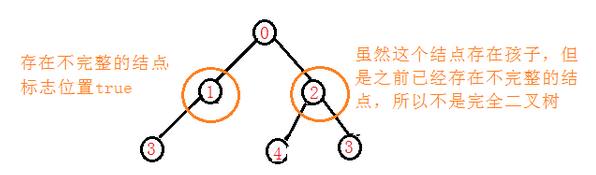
完全二叉树除最后一层外, 每一层的结点数均达到最大值, 在最后一层上只缺少右边的若干结点, 即最后一层的结点优先填在左边.
(b)是一棵完全二叉树, 如果结点12填在6的右边, 则该树不是完全二叉树.
完全二叉树的特点:
- 叶子结点只能出现在最下两层
- 最下层的叶子结点从左到右没有间隔, 如下图的反例
- 如果结点的度为1, 那么该结点不能出现只有右孩子的情况
- 同样结点数的二叉树, 完全二叉树的深度最小
满二叉树在每一层的结点数都是最大, 如果一棵深度为k的二叉树有2^k-1个结点, 那么这是一棵满二叉树.
满二叉树肯定是完全二叉树, 但是反之不成立.
一棵只有左孩子或只有右孩子的二叉树叫做斜树, 只有左孩子的称作左斜树, 只有有孩子的称作右斜树.
斜树的每一层只有一个结点, 结点的个数与二叉树的深度相同.
i = 1, 最多1个结点
i = 2, 最多2个结点
i = 3, 最多4个结点
...
k = 1, 最多1个结点
k = 2, 最多1 + 2个结点
k = 3, 最多1 + 2 + 4个结点
...
假设度为1的结点数为n1, 叶子数为n0, 总结点数为n
n = n2 + n1 + n0 = 2n2 + n1 + 1(根结点)
所以, n0 = n2+1
n = 1, 深度为1
n = 2或3, 深度2
n = 4/5/6/7, 深度为3
