堆结构与时间复杂度分析.md

堆结构与时间复杂度分析

目录

• 知识准备
• 定义
• 性质
• 将一棵完全二叉树构建为最大堆
• 构建堆的时间复杂度分析

知识准备

• 二叉树的概念、分类、性质

定义

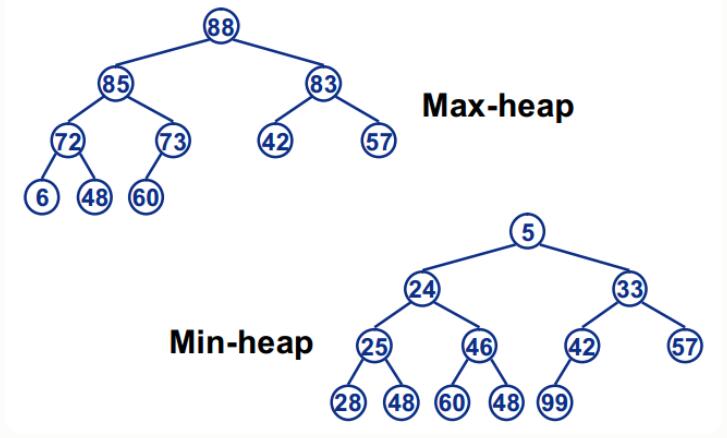
堆是一个利用完全二叉树的结构来维护的一维数组, 任意结点小于(或大于)它的左右子节点，最小值(或最大值)在根结点位置.
最小值在根节点(堆顶)的叫做小根(顶)堆, 最大值在根节点(堆顶)的叫做大根(顶)堆.

性质

堆可以看做是一棵完全二叉树的数组对象.
堆总是一棵完全二叉树.
堆中某个结点的值总是不大于或不小于其父结点的值.
堆的根结点是最小值或最大值.

将一棵完全二叉树构建为最大堆

如一个数组为: arr = [5, 1, 13, 3, 16, 7, 10, 14, 6, 9] , 它的完全二叉树结构如下图:

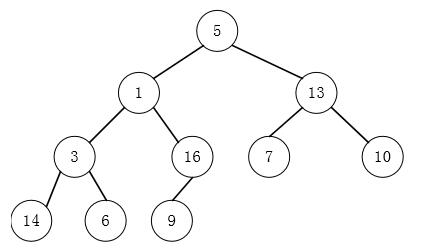
将该完全二叉树构建为最大堆的代码如下:
PHP

<?php

$arr = [5, 1, 13, 3, 16, 7, 10, 14, 6, 9];

for ($i = 1; $i < count($arr); $i++) {
    // 0 - i 区间形成大根堆
    heapInsert($arr, $i);
}

/**
 * 构建大根堆(加入一个结点并向上调整的过程)
 *
 * @param $arr
 * @param $index
 */
function heapInsert(&$arr, $index)
{
    while ($arr[$index] > $arr[intval(($index - 1) / 2)]) {
        // 父结点
        $parent = intval(($index - 1) / 2);
        // swap
        list($arr[$index], $arr[$parent]) = [$arr[$parent], $arr[$index]];
        // 索引来到父结点位置
        $index = $parent;
    }
}

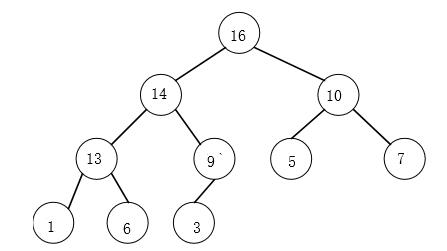
print_r($arr);

打印结果为:

Array
(
    [0] => 16
    [1] => 14
    [2] => 10
    [3] => 13
    [4] => 9
    [5] => 5
    [6] => 7
    [7] => 1
    [8] => 6
    [9] => 3
)

大根堆的创建结果如下图:

构建堆的时间复杂度分析

构建堆时, 从第二个结点开始向上调整, 第二个结点调整次数log2, 第三个结点调整次数log3, 第N个结点调整次数logN,
所以, 构建堆的时间复杂度为: log2 + log3 + ... + logN = O(N) , 其中O(N)是推导得出的结论.

参考

• https://www.cnblogs.com/bigdata-stone/p/10475423.html