Merge branch 'main' into sc/glm_speed_coupled_semis

docs/literate/src/files/first_steps/changing_trixi.jl

@@ -0,0 +1,77 @@
+#src # Changing Trixi.jl itself
+
+# If you plan on editing Trixi.jl itself, you can download Trixi.jl locally and run it from
+# the cloned directory.
+
+
+# ## Cloning Trixi.jl
+
+
+# ### Windows
+
+# If you are using Windows, you can clone Trixi.jl by using the GitHub Desktop tool:
+# - If you do not have a GitHub account yet, create it on
+#   the [GitHub website](https://github.com/join).
+# - Download and install [GitHub Desktop](https://desktop.github.com/) and then log in to
+#   your account.
+# - Open GitHub Desktop, press `Ctrl+Shift+O`.
+# - In the opened window, paste `trixi-framework/Trixi.jl` and choose the path to the folder where
+#   you want to save Trixi.jl. Then click `Clone` and Trixi.jl will be cloned to your computer. 
+
+# Now you cloned Trixi.jl and only need to tell Julia to use the local clone as the package sources:
+# - Open a terminal using `Win+r` and `cmd`. Navigate to the folder with the cloned Trixi.jl using `cd`.
+# - Create a new directory `run`, enter it, and start Julia with the `--project=.` flag:
+#   ```shell
+#   mkdir run 
+#   cd run
+#   julia --project=.
+#   ```
+# - Now run the following commands to install all relevant packages:
+#   ```julia
+#   using Pkg; Pkg.develop(PackageSpec(path="..")) # Tell Julia to use the local Trixi.jl clone
+#   Pkg.add(["OrdinaryDiffEq", "Plots"])  # Install additional packages
+#   ```
+
+# Now you already installed Trixi.jl from your local clone. Note that if you installed Trixi.jl
+# this way, you always have to start Julia with the `--project` flag set to your `run` directory,
+# e.g.,
+# ```shell
+# julia --project=.
+# ```
+# if already inside the `run` directory.
+
+
+# ### Linux
+
+# You can clone Trixi.jl to your computer by executing the following commands:
+# ```shell
+# git clone [email protected]:trixi-framework/Trixi.jl.git 
+# # If an error occurs, try the following:
+# # git clone https://github.com/trixi-framework/Trixi.jl
+# cd Trixi.jl
+# mkdir run 
+# cd run
+# julia --project=. -e 'using Pkg; Pkg.develop(PackageSpec(path=".."))' # Tell Julia to use the local Trixi.jl clone
+# julia --project=. -e 'using Pkg; Pkg.add(["OrdinaryDiffEq", "Plots"])' # Install additional packages
+# ```
+# Note that if you installed Trixi.jl this way,
+# you always have to start Julia with the `--project` flag set to your `run` directory, e.g.,
+# ```shell
+# julia --project=.
+# ```
+# if already inside the `run` directory.
+
+
+# ## Additional reading
+
+# To further delve into Trixi.jl, you may have a look at the following introductory tutorials.
+# - [Introduction to DG methods](@ref scalar_linear_advection_1d) will teach you how to set up a
+#   simple way to approximate the solution of a hyperbolic partial differential equation. It will
+#   be especially useful to learn about the 
+#   [Discontinuous Galerkin method](https://en.wikipedia.org/wiki/Discontinuous_Galerkin_method)
+#   and the way it is implemented in Trixi.jl.
+# - [Adding a new scalar conservation law](@ref adding_new_scalar_equations) and
+#   [Adding a non-conservative equation](@ref adding_nonconservative_equation)
+#   describe how to add new physics models that are not yet included in Trixi.jl.
+# - [Callbacks](@ref callbacks-id) gives an overview of how to regularly execute specific actions
+#   during a simulation, e.g., to store the solution or adapt the mesh.

docs/literate/src/files/first_steps/create_first_setup.jl

@@ -0,0 +1,268 @@
+#src # Create first setup
+
+# In this part of the introductory guide, we will create a first Trixi.jl setup as an extension of
+# [`elixir_advection_basic.jl`](https://github.com/trixi-framework/Trixi.jl/blob/main/examples/tree_2d_dgsem/elixir_advection_basic.jl).
+# Since Trixi.jl has a common basic structure for the setups, you can create your own by extending
+# and modifying the following example.
+
+# Let's consider the linear advection equation for a state ``u = u(x, y, t)`` on the two-dimensional spatial domain
+# ``[-1, 1] \times [-1, 1]`` with a source term
+# ```math
+# \frac{\partial}{\partial t}u + \frac{\partial}{\partial x} (0.2 u) - \frac{\partial}{\partial y} (0.7 u) = - 2 e^{-t}
+# \sin\bigl(2 \pi (x - t) \bigr) \sin\bigl(2 \pi (y - t) \bigr),
+# ```
+# with the initial condition
+# ```math
+# u(x, y, 0) = \sin\bigl(\pi x \bigr) \sin\bigl(\pi y \bigr),
+# ```
+# and periodic boundary conditions.
+
+# The first step is to create and open a file with the .jl extension. You can do this with your
+# favorite text editor (if you do not have one, we recommend [VS Code](https://code.visualstudio.com/)).
+# In this file you will create your setup.
+
+# To be able to use functionalities of Trixi.jl, you always need to load Trixi.jl itself
+# and the [OrdinaryDiffEq.jl](https://github.com/SciML/OrdinaryDiffEq.jl) package.
+
+using Trixi
+using OrdinaryDiffEq
+
+# The next thing to do is to choose an equation that is suitable for your problem. To see all the
+# currently implemented equations, take a look at
+# [`src/equations`](https://github.com/trixi-framework/Trixi.jl/tree/main/src/equations).
+# If you are interested in adding a new physics model that has not yet been implemented in
+# Trixi.jl, take a look at the tutorials
+# [Adding a new scalar conservation law](@ref adding_new_scalar_equations) or
+# [Adding a non-conservative equation](@ref adding_nonconservative_equation).
+
+# The linear scalar advection equation in two spatial dimensions
+# ```math
+# \frac{\partial}{\partial t}u + \frac{\partial}{\partial x} (a_1 u) + \frac{\partial}{\partial y} (a_2 u) = 0
+# ```
+# is already implemented in Trixi.jl as
+# [`LinearScalarAdvectionEquation2D`](@ref), for which we need to define a two-dimensional parameter
+# `advection_velocity` describing the parameters ``a_1`` and ``a_2``. Appropriate for our problem is `(0.2, -0.7)`.
+
+advection_velocity = (0.2, -0.7)
+equations = LinearScalarAdvectionEquation2D(advection_velocity)
+
+# To solve our problem numerically using Trixi.jl, we have to discretize the spatial
+# domain, for which we set up a mesh. One of the most used meshes in Trixi.jl is the
+# [`TreeMesh`](@ref). The spatial domain used is ``[-1, 1] \times [-1, 1]``. We set an initial number
+# of elements in the mesh using `initial_refinement_level`, which describes the initial number of
+# hierarchical refinements. In this simple case, the total number of elements is `2^initial_refinement_level`
+# throughout the simulation. The variable `n_cells_max` is used to limit the number of elements in the mesh,
+# which cannot be exceeded when using [adaptive mesh refinement](@ref Adaptive-mesh-refinement).
+
+# All minimum and all maximum coordinates must be combined into `Tuples`.
+
+coordinates_min = (-1.0, -1.0)
+coordinates_max = ( 1.0,  1.0)
+mesh = TreeMesh(coordinates_min, coordinates_max,
+                initial_refinement_level = 4,
+                n_cells_max = 30_000)
+
+# To approximate the solution of the defined model, we create a [`DGSEM`](@ref) solver.
+# The solution in each of the recently defined mesh elements will be approximated by a polynomial
+# of degree `polydeg`. For more information about discontinuous Galerkin methods,
+# check out the [Introduction to DG methods](@ref scalar_linear_advection_1d) tutorial.
+
+solver = DGSEM(polydeg=3)
+
+# Now we need to define an initial condition for our problem. All the already implemented
+# initial conditions for [`LinearScalarAdvectionEquation2D`](@ref) can be found in
+# [`src/equations/linear_scalar_advection_2d.jl`](https://github.com/trixi-framework/Trixi.jl/blob/main/src/equations/linear_scalar_advection_2d.jl).
+# If you want to use, for example, a Gaussian pulse, it can be used as follows:
+# ```julia
+# initial_conditions = initial_condition_gauss
+# ```
+# But to show you how an arbitrary initial condition can be implemented in a way suitable for
+# Trixi.jl, we define our own initial conditions.
+# ```math
+# u(x, y, 0) = \sin\bigl(\pi x \bigr) \sin\bigl(\pi y \bigr).
+# ```
+# The initial conditions function must take spatial coordinates, time and equation as arguments
+# and returns an initial condition as a statically sized vector `SVector`. Following the same structure, you
+# can define your own initial conditions. The time variable `t` can be unused in the initial
+# condition, but might also be used to describe an analytical solution if known. If you use the
+# initial condition as analytical solution, you can analyze your numerical solution by computing
+# the error, see also the
+# [section about analyzing the solution](https://trixi-framework.github.io/Trixi.jl/stable/callbacks/#Analyzing-the-numerical-solution).
+
+function initial_condition_sinpi(x, t, equations::LinearScalarAdvectionEquation2D)
+    scalar = sinpi(x[1]) * sinpi(x[2])
+    return SVector(scalar)
+end
+initial_condition = initial_condition_sinpi
+
+# The next step is to define a function of the source term corresponding to our problem.
+# ```math
+# f(u, x, y, t) = - 2 e^{-t} \sin\bigl(2 \pi (x - t) \bigr) \sin\bigl(2 \pi (y - t) \bigr)
+# ```
+# This function must take the state variable, the spatial coordinates, the time and the
+# equation itself as arguments and returns the source term as a static vector `SVector`.
+
+function source_term_exp_sinpi(u, x, t, equations::LinearScalarAdvectionEquation2D)
+    scalar = - 2 * exp(-t) * sinpi(2*(x[1] - t)) * sinpi(2*(x[2] - t))
+    return SVector(scalar)
+end
+
+# Now we collect all the information that is necessary to define a spatial discretization,
+# which leaves us with an ODE problem in time with a span from 0.0 to 1.0.
+# This approach is commonly referred to as the method of lines. 
+
+semi = SemidiscretizationHyperbolic(mesh, equations, initial_condition, solver;
+                                    source_terms = source_term_exp_sinpi)
+tspan = (0.0, 1.0)
+ode = semidiscretize(semi, tspan);
+
+# At this point, our problem is defined. We will use the `solve` function defined in
+# [OrdinaryDiffEq.jl](https://github.com/SciML/OrdinaryDiffEq.jl) to get the solution.
+# OrdinaryDiffEq.jl gives us the ability to customize the solver
+# using callbacks without actually modifying it. Trixi.jl already has some implemented
+# [Callbacks](@ref callbacks-id). The most widely used callbacks in Trixi.jl are
+# [step control callbacks](https://docs.sciml.ai/DiffEqCallbacks/stable/step_control/) that are
+# activated at the end of each time step to perform some actions, e.g. to print statistics.
+# We will show you how to use some of the common callbacks.
+
+# To print a summary of the simulation setup at the beginning
+# and to reset timers we use the [`SummaryCallback`](@ref).
+# When the returned callback is executed directly, the current timer values are shown.
+
+summary_callback = SummaryCallback()
+
+# We also want to analyze the current state of the solution in regular intervals.
+# The [`AnalysisCallback`](@ref) outputs some useful statistical information during the solving process
+# every `interval` time steps.
+
+analysis_callback = AnalysisCallback(semi, interval = 5)
+
+# It is also possible to control the time step size using the [`StepsizeCallback`](@ref) if the time
+# integration method isn't adaptive itself. To get more details, look at
+# [CFL based step size control](@ref CFL-based-step-size-control).
+
+stepsize_callback = StepsizeCallback(cfl = 1.6)
+
+# To save the current solution in regular intervals we use the [`SaveSolutionCallback`](@ref).
+# We would like to save the initial and final solutions as well. The data
+# will be saved as HDF5 files located in the `out` folder. Afterwards it is possible to visualize
+# a solution from saved files using Trixi2Vtk.jl and ParaView, which is described below in the
+# section [Visualize the solution](@ref Visualize-the-solution).
+
+save_solution = SaveSolutionCallback(interval = 5,
+                                     save_initial_solution = true,
+                                     save_final_solution = true)
+
+# Alternatively, we have the option to print solution files at fixed time intervals. 
+# ```julua
+# save_solution = SaveSolutionCallback(dt = 0.1,
+#                                      save_initial_solution = true,
+#                                      save_final_solution = true)
+# ```
+
+# Another useful callback is the [`SaveRestartCallback`](@ref). It saves information for restarting
+# in regular intervals. We are interested in saving a restart file for the final solution as
+# well. To perform a restart, you need to configure the restart setup in a special way, which is
+# described in the section [Restart simulation](@ref restart).
+
+save_restart = SaveRestartCallback(interval = 100, save_final_restart = true)
+
+# Create a `CallbackSet` to collect all callbacks so that they can be passed to the `solve`
+# function.
+
+callbacks = CallbackSet(summary_callback, analysis_callback, stepsize_callback, save_solution,
+                        save_restart)
+
+# The last step is to choose the time integration method. OrdinaryDiffEq.jl defines a wide range of
+# [ODE solvers](https://docs.sciml.ai/DiffEqDocs/latest/solvers/ode_solve/), e.g.
+# `CarpenterKennedy2N54(williamson_condition = false)`. We will pass the ODE
+# problem, the ODE solver and the callbacks to the `solve` function. Also, to use
+# `StepsizeCallback`, we must explicitly specify the initial trial time step `dt`, the selected
+# value is not important, because it will be overwritten by the `StepsizeCallback`. And there is no
+# need to save every step of the solution, we are only interested in the final result.
+
+sol = solve(ode, CarpenterKennedy2N54(williamson_condition = false), dt = 1.0,
+            save_everystep = false, callback = callbacks);
+
+# Finally, we print the timer summary.
+
+summary_callback()
+
+# Now you can plot the solution as shown below, analyze it and improve the stability, accuracy or
+# efficiency of your setup.
+
+
+# ## Visualize the solution
+
+# In the previous part of the tutorial, we calculated the final solution of the given problem, now we want
+# to visualize it. A more detailed explanation of visualization methods can be found in the section
+# [Visualization](@ref visualization).
+
+
+# ### Using Plots.jl
+
+# The first option is to use the [Plots.jl](https://github.com/JuliaPlots/Plots.jl) package
+# directly after calculations, when the solution is saved in the `sol` variable. We load the
+# package and use the `plot` function.
+
+using Plots
+plot(sol)
+
+# To show the mesh on the plot, we need to extract the visualization data from the solution as
+# a [`PlotData2D`](@ref) object. Mesh extraction is possible using the [`getmesh`](@ref) function.
+# Plots.jl has the `plot!` function that allows you to modify an already built graph.
+
+pd = PlotData2D(sol)
+plot!(getmesh(pd))
+
+
+# ### Using Trixi2Vtk.jl
+
+# Another way to visualize a solution is to extract it from a saved HDF5 file. After we used the
+# `solve` function with [`SaveSolutionCallback`](@ref) there is a file with the final solution.
+# It is located in the `out` folder and is named as follows: `solution_index.h5`. The `index`
+# is the final time step of the solution that is padded to 6 digits with zeros from the beginning.
+# With [Trixi2Vtk](@ref) you can convert the HDF5 output file generated by Trixi.jl into a VTK file.
+# This can be used in visualization tools such as [ParaView](https://www.paraview.org) or
+# [VisIt](https://visit.llnl.gov) to plot the solution. The important thing is that currently
+# Trixi2Vtk.jl supports conversion only for solutions in 2D and 3D spatial domains.
+
+# If you haven't added Trixi2Vtk.jl to your project yet, you can add it as follows.
+# ```julia
+# import Pkg
+# Pkg.add(["Trixi2Vtk"])
+# ```
+# Now we load the Trixi2Vtk.jl package and convert the file `out/solution_000018.h5` with
+# the final solution using the [`trixi2vtk`](@ref) function saving the resulting file in the
+# `out` folder.
+
+using Trixi2Vtk
+trixi2vtk(joinpath("out", "solution_000018.h5"), output_directory="out")
+
+# Now two files `solution_000018.vtu` and `solution_000018_celldata.vtu` have been generated in the
+# `out` folder. The first one contains all the information for visualizing the solution, the
+# second one contains all the cell-based or discretization-based information.
+
+# Now let's visualize the solution from the generated files in ParaView. Follow this short
+# instruction to get the visualization.
+# - Download, install and open [ParaView](https://www.paraview.org/download/).
+# - Press `Ctrl+O` and select the generated files `solution_000018.vtu` and
+#   `solution_000018_celldata.vtu` from the `out` folder.
+# - In the upper-left corner in the Pipeline Browser window, left-click on the eye-icon near
+#   `solution_000018.vtu`.
+# - In the lower-left corner in the Properties window, change the Coloring from Solid Color to
+#   scalar. This already generates the visualization of the final solution.
+# - Now let's add the mesh to the visualization. In the upper-left corner in the
+#   Pipeline Browser window, left-click on the eye-icon near `solution_000018_celldata.vtu`.
+# - In the lower-left corner in the Properties window, change the Representation from Surface
+#   to Wireframe. Then a white grid should appear on the visualization.
+# Now, if you followed the instructions exactly, you should get a similar image as shown in the
+# section [Using Plots.jl](@ref Using-Plots.jl):
+
+# ![paraview_trixi2vtk_example](https://github.com/trixi-framework/Trixi.jl/assets/119304909/0c29139b-6c5d-4d5c-86e1-f4ebc95aca7e)
+
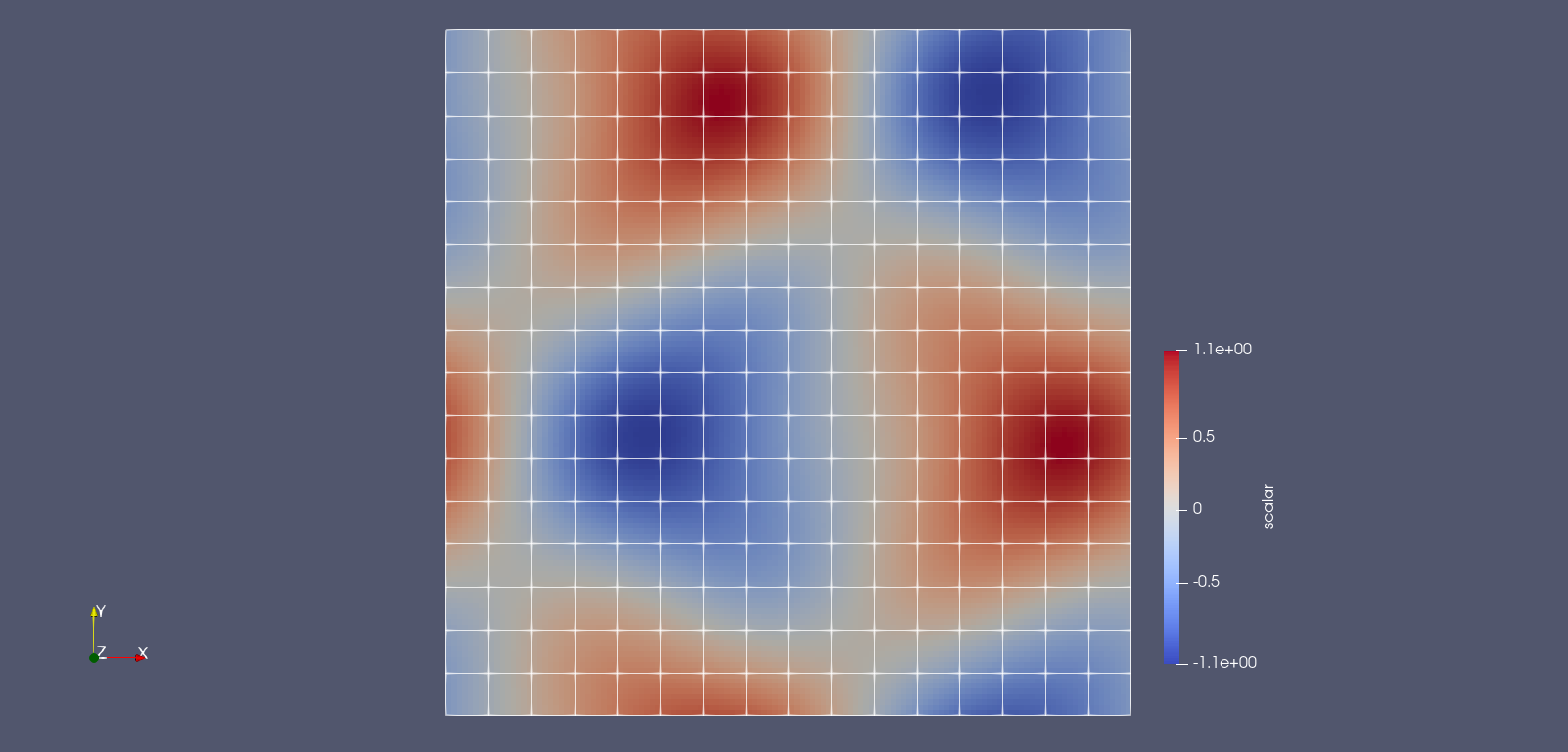+# After completing this tutorial you are able to set up your own simulations with
+# Trixi.jl. If you have an interest in contributing to Trixi.jl as a developer, refer to the third
+# part of the introduction titled [Changing Trixi.jl itself](@ref changing_trixi).
+
+Sys.rm("out"; recursive=true, force=true) #hide #md