Module Geometry

Geometric Data Structures

The following image shows a simplified overview of the hierarchy of the main geometry classes in GoTools.

All geometric objects are of type GeomObject. This class has a function instanceType, and by calling this function, it is possible to check the concrete type of a given object. A GeomObject is Streamable, which means that they can be written to and read from a stream (typically a file) in a uniform way. See the GoTools g2-file format documentation for more information on this topic. Similarly, they can be created in a uniform way by the Factory, which is useful when you want to generate objects whose exact kind is unknown at compile time.

Parametric Curves

ParamCurve is the base class for all parametric curves in GoTools and defines a common interface. Many operations do not need to distinguish between different types of parametric curves. A parametric curve has (with some exceptions) the following functionality:

• operations on the curve
  • clone: make a copy of this curve
  • subCurve: create a subcurve of this curve
  • appendCurve: append another curve to this curve
  • split: split the curve into two curves at a given parameter
• operations in the parameter interval
  • startparam: fetch start parameter
  • endparam: fetch end parameter
  • setParameterInterval: linearly reparametrize the parameter interval
  • reverseParameterDirection: reverse the parameter interval
• evaluations
  • point: evaluate the curve's position (and perhaps a certain number of derivatives) at a given parameter
  • uniformEvaluator: evaluate the curve's position at a regular set of parameter values
• geometric information retrieval
  • length: compute the length of (a segment of) the curve
  • estimatedCurveLength: estimate the length of (a segment of) the curve
  • compositeBox: compute a composite box (bounding box) enclosing the curve
  • directionCone: compute a directional cone containing all tangent directions of this curve
• closest point computations
  • closestPointGeneric: compute the closest point on (a segment of) this curve to a specified point --- generic implementation
  • closestPoint: compute the closest point on (a segment of) this curve to a specified point --- specific implementation for each parametric curve type
• checks for degeneracy, symmetry, and type
  • isLinear: check if the curve is linear
  • isInPlane: check if the curve is contained in a plane belonging to a given pencil of planes
  • isAxisRotational: check if the curve is axis rotational
  • isDegenerate: check whether the curve degenerates to a single point
  • isClosed: check whether the curve is closed

Parametric Surfaces

ParamSurface is the base class for a parametric surface and defines the common interface for all parametric surfaces. A parametric surface has (with some exceptions) the following functionality:

• operations on the surface
  • clone: make a copy of this surface
  • subSurfaces: create subsurfaces of this surface
  • asSplineSurface: create a spline surface represented by this surface, if any
  • outerBoundaryLoop: fetch the anticlockwise, outer boundary loop of the surface
  • allBoundaryLoops: fetch the anticlockwise outer boundary loop of the surface, together with clockwise loops of any interior boundaries
  • getBoundaryInfo: compute the boundary curve segment between two points on the boundary, as well as the cross-tangent curve
  • mirrorSurface: reflect the surface through a given plane
  • getInternalPoint: fetch an (unspecified) internal point in the surface
  • constParamCurves: fetch the curve(s) obtained by intersecting the surface with one of its isoparametric curves
  • nextSegmentVal: determine the parameter value of the start of the 'next segment' from a parameter value, along a given parameter direction
  • turnOrientation: flip the direction of the normal of the surface
  • getCornerPoints: fetch surface corners, geometric and parametric points
• operations in the parameter domain
  • setParameterDomain: set the parameter domain to a given rectangle
  • parameterDomain: fetch the parameter domain
  • containingDomain: fetch a rectangular domain that contains the parameter domain
  • inDomain: check if a parameter pair lies in the parameter domain
  • inDomain2: check if a parameter pair lies inside, on the boundary, or outside of the parameter domain
  • onBoundary: check if a parameter pair lies on the boundary of the parameter domain
  • closestInDomain: fetch the parameter value in the parameter domain closest to a given parameter pair
  • reverseParameterDirection: reverse one of the parameter directions
  • swapParameterDirection: swap the two parameter directions
• geometric information retrieval
  • normalCone: create a direction cone containing all surface normals
  • tangentCone: create a direction cone containing all surface tangents in a given parameter direction
  • compositeBox: compute a composite box (bounding box) enclosing the surface
  • area: compute the total area of this surface
  • estimateSfSize: estimate the size of the surface in the two parameter directions
• evaluations
  • point: evaluate the surface's position (and perhaps a certain number of derivatives) at a given parameter pair
  • normal: evaluate the surface normal for a given parameter pair
  • evalGrid: evaluate the surface's position at a grid in the parameter domain
• closest point computations
  • closestPoint: iteratively find the closest point on the surface to a given point
  • closestBoundaryPoint: iteratively find the closest point on the boundary of the surface to a given point
  • setIterator: set type of closest point iterator
• checks for degeneracy, symmetry, and type
  • isDegenerate: check whether one of the four boundary curves is degenerate (i.e., has zero length)
  • getDegenerateCorners: find degenerate surface corners by checking for parallel and anti-parallel partial derivatives
  • isIsoTrimmed: check if the surface is trimmed along constant parameter curves
  • isSpline: check if the surface is of type spline
  • isAxisRotational: check if the surface is axis rotational
  • isPlanar: check if the surface is planar
  • isLinear: check if the surface is linear in one or both directions
  • ElementOnBoundary: check if a polynomial element (for spline surfaces) intersects the (trimming) boundaries
  • ElementBoundaryStatus : check if a polynomial element (for spline surfaces) intersects the (trimming) boundaries, is inside or outside

B-spline Curves

A B-spline curve is represented by the SplineCurve class.

Mathematically, the curve is defined by the parametrization

$$ {\bf c}(t) = \sum_{i=1}^{n} {\bf p}_{i} B_{i,k,{\bf t}}(t). $$

The dimension $dim$ of the curve ${\bf c}$ is equal to that of its control points ${\bf p}_i$. For example, if the dimension of the control points is one, the curve is a function, if the dimension is two, the curve is planar, and if the dimension is three, the curve is spatial. Usually the dimension of the curve will be at most three, but higher dimensions are allowed.

A B-spline curve is a linear combination of a sequence of B-splines $B_{i,k,{\bf t}}$ (called a B-basis) uniquely determined by a knot vector ${\bf t}$ and the order $k$. The order is equal to the polynomial degree plus one. For example, if the order is two, the degree is one and the B-splines and the curve $c$ they generate are (piecewise) linear. If the order is three, the degree is two and the B-splines and the curve are quadratic. Cubic B-splines and curves have order 4 and degree 3, etc.

The parameter range of a B-spline curve ${\bf c}$ is the interval $[t_k, t_{n+1}], $ and so mathematically, the curve is a mapping ${\bf c}: [t_k, t_{n+1}] \to {\bf R}^{dim}$, where $dim$ is the Euclidean space dimension of its control points.

The complete representation of a B-spline curve consists of

• $dim$: The dimension of the underlying Euclidean space, $1,2,3,\ldots$.
• $n$: The number of control points (also the number of B-splines)
• $k$: The order (polynomial degree + 1) of the B-splines.
• ${\bf t}$: The knot vector of the B-splines. ${\bf t} = (t_1, t_2, \ldots, t_{n+k})$.
• ${\bf p}$: The control points of the B-spline curve. $p_{d,i}, d=1,\ldots,dim, i=1,\ldots,n.$ E.g. when $dim = 3$, we have ${\bf p} = (x_1,y_1,z_1,x_2,y_2,z_2,\ldots,x_n,y_n,z_n)$.

We note that arrays in $c$ start at index 0 which means, for example, that if the array $t$ holds the knot vector, then $t[0] = t_1,\ldots, t[n+k-1] = t_{n+k}$ and the parameter interval goes from $t[k-1]$ to $t[n]$. Similar considerations apply to the other arrays.

The data in the curve representation must satisfy certain conditions:

• The knot vector must be non-decreasing: $t_i \le t_{i+1}$. Moreover, the knots $t_i$ and $t_{i+k}$ must be distinct: $t_i < t_{i+k}$.
• The number of control points should be greater than or equal to the order of the curve: $n \ge k$.

To understand the representation better, we will look at three parts of the representation: the B-splines (the basis functions), the knot vector and the control polygon.

B-spline Basis Functions

The spline space is represented by the class BsplineBasis. A set of B-spline basis functions is determined by the order $k$ and the knots.

Linear B-splines

For example, to define a single basis function of degree one, we need three knots.

A linear B-spline (order 2) defined by three knots

In the figure the three knots are marked as dots.

Linear B-splines with multiple knots at one end

In the figure above the two knots at each end are equal.

By taking a linear combination of the three basis functions shown above, we can generate a linear spline function as shown in the next figure.

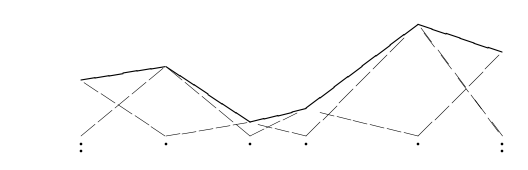
A linear B-spline curve of dimension 1 (solid) as a linear combination of a sequence of B-splines. Each B-spline (dashed) is scaled by a coefficient.

Quadratic B-splines

A quadratic B-spline basis function is a linear combination of two linear basis functions, in which the coefficients are linear affine in the parameter $t$. In the next figure, we will see a quadratic B-spline defined by four knots. A quadratic B-spline is the sum of two products, the first product between the linear B-spline on the left and a corresponding line from 0 to 1, the second product between the linear B-spline on the right and a corresponding line from 1 to 0.

A quadratic B-spline (solid) as a weighted (dashed) linear combination of linear B-splines (solid)

Higher-order B-splines

For higher-order B-splines there is a similar definition. A B-spline of order $k\geq 2$ is a weighted linear combination of two B-splines of order $k-1$. Explicitly, we define B-splines of order $k=1$ as box functions,

$$ B_{i,1}(t) = 1 \quad \text{if} \quad t_i \leq t < t_{i+1} \quad \text{and} \quad 0 \quad \text{otherwise}, $$

and then the B-splines of order $k\geq 2$ as

$$ B_{i,k}(t) = {t - t_i \over t_{i+k-1} - t_i} B_{i,k-1}(t) + {t_{i+k} - t \over t_{i+k} - t_{i+1}} B_{i-1,k-1}(t). $$

Basic properties

B-spline basis functions satisfy some important properties for curve and surface design. Each basis function is non-negative and it can be shown that they sum to one,

$$ \sum_{i=1}^{n}B_{i,k,{\bf t}}(t) = 1. $$

These properties combined mean that B-spline curves satisfy the convex hull property: the curve lies in the convex hull of its control points. Furthermore, the support of the B-spline basis function $B_{i,k,{\bf t}}$ is the interval $[t_i,t_{i+k}]$ which means that B-spline curves has local control: moving one control point only alters the curve locally.

With $k$ multiple knots at the ends of the knot vector, B-spline curves also have the endpoint property: the start point of the B-spline curve equals the first control point and the end point equals the last control point, in other words

$$ {\bf c}(t_k) = {\bf p}_1 \qquad \hbox{and} \qquad {\bf c}(t_{n+1}) = {\bf p}_n. $$

The Control Polygon

The control polygon of a B-spline curve is the polygonal arc formed by its control points, ${\bf p}_0, {\bf p}_1, \ldots,{\bf p}_n$. This means that the control polygon, regarded as a parametric curve, is itself a piecewise linear B-spline curve (order two), identical to its own control polygon. If we increase the order, the distance between the control polygon and the curve increases. A higher order B-spline curve tends to smooth the control polygon and at the same time mimic its shape. For example, if the control polygon is convex, so is the B-spline curve.

Linear, quadratic, and cubic planar B-spline curves sharing the same control polygon

Another property of the control polygon is that it will get closer to the curve if it is redefined by inserting knots into the curve and thereby increasing the number of control points. This can be seen in the next figure. In the limit, the refinement of the control polygon converges to its B-spline curve.

The cubic B-spline curve shown above with a redefined knot vector

The Knot Vector

The knots of a B-spline curve describe the following properties of the curve:

• The parameterization of the B-spline curve
• The continuity at the joins between the adjacent polynomial segments of the B-spline curve.

Although the curves in the figure below have the same control polygon, they have different knot vectors and therefore different parametrizations.

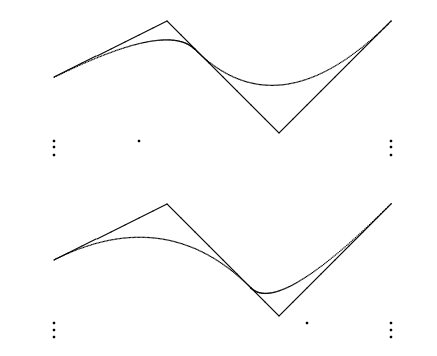
Two quadratic planar B-spline curves with identical control polygons but different knot vectors

This example is not meant as an encouragement to use parameterization for modelling, rather to make users aware of the effect of parameterization. Something close to curve length parameterization is in most cases preferable. For interpolation, chord-length parameterization is used in most cases.

The number of equal knots determines the degree of continuity. If $k$ consecutive internal knots are equal, the curve is discontinuous. Similarly if $k-1$ consecutive internal knots are equal, the curve is continuous but not in general differentiable. A continuously differentiable curve with a discontinuity in the second derivative can be modelled using $k-2$ equal knots etc. Normally, B-spline curves in GoTools are expected to be continuous. For many algorithms, curves should be continuously differentiable ($C^1$).

A quadratic B-spline curve with two inner knots

NURBS Curves

A NURBS (Non-Uniform Rational B-Spline) curve is a generalization of a B-spline curve,

$$ {\bf c}(t) = {\sum_{i=1}^{n} w_i {\bf p}_i B_{i,k,{\bf t}}(t) \over \sum_{i=1}^{n} w_i B_{i,k,{\bf t}}(t)} . $$

In addition to the data of a B-spline curve, the NURBS curve ${\bf c}$ has a sequence of weights $w_1,\ldots,w_n$. One of the advantages of NURBS curves over B-spline curves is that they can be used to represent conic sections exactly (taking the order $k$ to be three). A disadvantage is that NURBS curves depend nonlinearly on their weights, making some calculations, like the evaluation of derivatives, more complicated and less efficient than with B-spline curves.

The representation of a NURBS curve is the same as for a B-spline curve except that it also includes

• ${\bf w}$: A sequence of weights ${\bf w} = (w_1, w_2, \ldots, w_n)$.

We make the assumption that the weights are strictly positive: $w_i &gt; 0$.

Under this condition, a NURBS curve, like its B-spline cousin, enjoys the convex hull property. With $k$-fold knots at the ends of the knot vector, also NURBS curves have the endpoint interpolation property.

A NURBS curve is in GoTools stored using the same entities as non-rational spline curves. Note that the constructors of these entities assume that the NURBS coefficients are given in the format: $w_i p_{i,1}, \ldots w_i p_{i,dim},w_i$, for $i=1, \ldots n$, i.e., the coefficients are multiplied with the weigths.

Spline Curve Functionality

In GoTools, SplineCurve inherites ParamCurve and has thereby the functionality specified for ParamCurve objects. Functionality specific for a B-spline curve can be found in the doxygen information. This functionality includes:

• Compute the derivative curve corresponding to a given curve
• Fetch information related to the spline space
• Fetch the control polygon of a spline curve
• Insert new knots into the knot vector of the curve and update the curve accordingly
• Increase the polynomial degree of the curve
• Make sure that the curve has got an open knot vector, i.e., knot multiplicity equal to the order in the ends of the curve

B-spline Surfaces

A tensor product B-spline surface is represented by the class SplineSurface.

Mathematically, the B-spline surface is defined by the parametrization

$$ {\bf s}(u,v) = \sum_{i=1}^{n_1}\sum_{j=1}^{n_2}{\bf p}_{i,j} B_{i,k_1,{\bf u}}(u) B_{j,k_2,{\bf v}}(v) $$

with control points ${\bf p}_{i,j}$ and two variables (or parameters) $u$ and $v$. The formula shows that a basis function of a B-spline surface is a product of two basis functions of B-spline curves (B-splines). This is why a B-spline surface is called a tensor-product surface. The following is a list of the components of the representation:

• $dim$: The dimension of the underlying Euclidean space.
• $n_1$: The number of control points with respect to the first parameter.
• $n_2$: The number of control points with respect to the second parameter.
• $k_1$: The order (polynomial degree + 1) of the B-splines in the first parameter.
• $k_2$: The order of the B-splines in the second parameter.
• ${\bf u}$: The knot vector of the B-splines with respect to the first parameter, ${\bf u} = (u_1,u_2,\ldots,u_{n_1+k_1})$.
• ${\bf v}$: The knot vector of the B-splines with respect to the second parameter, ${\bf v} = (v_1,v_2,\ldots,v_{n_2+k_2})$.
• ${\bf p}$: The control points of the B-spline surface, $c_{d,i,j}$, $d=1,\ldots,dim$, $i=1,\ldots,n_1$, $j=1,\ldots,n_2$. When $dim = 3$, we have ${\bf p} = (x_{1,1},y_{1,1},z_{1,1},x_{2,1},y_{2,1},z_{2,1},\ldots$, $x_{n_1,1},y_{n_1,1},z_{n_1,1},\ldots$, $x_{n_1,n_2},y_{n_1,n_2},z_{n_1,n_2})$.

The data of the B-spline surface must fulfill the following requirements:

• Both knot vectors must be non-decreasing.
• The number of control points must be greater than or equal to the order with respect to both parameters: $n_1 \ge k_1$ and $n_2 \ge k_2$.

The properties of the representation of a B-spline surface are similar to the properties of the representation of a B-spline curve. The control points ${\bf p}_{i,j}$ form a control net as shown in the figure below. The control net has similar properties to the control polygon of a B-spline curve, described above.

A B-spline surface and its control net

The Basis Functions

A basis function of a B-spline surface is the product of two basis functions corresponding to B-spline curves,

$ B_{i,k_1,{\bf u}}(u) B_{j,k_2,{\bf v}}(v). $

Its support is the rectangle $[u_i,u_{i+k_1}] \times [v_j,v_{j+k_2}]$. If the basis functions in both directions are of degree one and all knots have multiplicity one, then the surface basis functions are pyramid-shaped. For higher degrees, the surface basis functions are bell shaped.

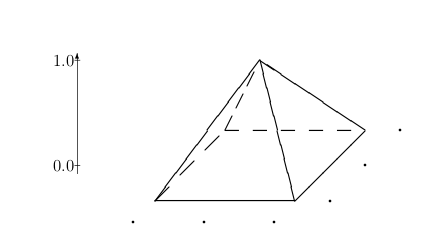
A basis function of degree one in both variables

NURBS Surfaces

A NURBS (Non-Uniform Rational B-Spline) surface is a generalization of a B-spline surface,

$$ {\bf s}(u,v) = {\sum_{i=1}^{n_1}\sum_{j=1}^{n_2} w_{i,j} {\bf p}_{i,j} B_{i,k_1,{\bf u}}(u) B_{j,k_2,{\bf v}}(v) \over \sum_{i=1}^{n_1}\sum_{j=1}^{n_2} w_{i,j} B_{i,k_1,{\bf u}}(u) B_{j,k_2,{\bf v}}(v)}. $$

In addition to the data of a B-spline surface, the NURBS surface has a weights $w_{i,j}$. NURBS surfaces can be used to exactly represent several common rational surfaces such as spheres, cylinders, tori, and cones. A disadvantage is that NURBS surfaces depend nonlinearly on their weights, making some calculations less efficient.

The representation of a NURBS surface is the same as for a B-spline surface except that it also includes

• ${\bf w}$: The weights of the NURBS surface, $w_{i,j}$, $i=1,\ldots,n_1$, $j=1,\ldots,n_2$, so ${\bf w} = (w_{1,1},w_{2,1},\ldots,w_{n_1,1},\ldots$, $w_{1,2},\ldots,w_{n_1,n_2})$.

The weights are required to be strictly positive: $w_{i,j} &gt; 0$.

The NURBS surface is represented by SISLSurf and SplineSurface in SISL and GoTools, respectively. As for the curve case, the constructors of SISLSurf and SplineSurface expect the coefficients to be multiplied with the weights.

Spline Surface Functionality

SplineSurface inherites ParamSurface in the GoTools data structure and implements the functionality described for ParamSurface. Important additional functionality is listed below:

• Compute the derivative surface and normal surface corresponding to a given surface
• Fetch information related to the spline spaces
• Fetch the control polygon of a spline surface
• Fetch all weights of a NURBS surface
• Grid evaluation of the basis functions related to a surface
• Grid evaluation of the surface
• Insert new knots into the knot vectors of the surface and adapt the surface description accordingly
• Increase the polynomial degrees of the surface
• Fetch information related to the boundary curves of a surface

Other Curve Types

As shown in the class hierarchy, a spline curve is not the only parametric curve in GoTools although it is the most important one. There are also other curves that share parts of the public interface:

• BoundedCurve A bounded curve is a restriction of a parametric curve to a given interval. The interval can be specified either in parameter space, in geometry space or both. In the last case, it must be specified whether the parameter space bound or the geometry space bound is the master.
• ElementaryCurve An elementary curve is a container for a conic section or a line. This entity will be described in some detail later.
• CurveOnSurface This class represents a curve lying on a surface.

Curve On Surface

The CurveOnSurface entity is often related to a bounded, or trimmed, surface. A bounded surface is limited by a curve loop where each curve in the loop most often is represented by a CurveOnSurface. However, a CurveOnSurface is an entity in its own right. It simply represents a curve lying on a surface. It can for instance originate from intersecting the surface with a plane.

A CurveOnSurface consists of a parametric surface and two corresponding curves, one curve in the parameter domain of the surface and one spatial curve. The master representation is specified. Some operations may required the existence of one particular of these curves, in particular the parameter curve is requested. It exists functions that compute the missing curve from the existing one.

Elementary Curve

An ElementaryCurve is a fairly new concept in GoTools, and until now such curves have been entered as entities in an IGES or STEP file. The elementary curves may also be represented as spline curves although non-bounded curves must be given a finite extension. The elementary curves is of the types:

• Circle The circle is defined by its center and radius and the plane in which it lies if the dimension of the geometry space is larger than 2. A circle is parameterized in terms of the angle. This is a bounded parameterization.
• Ellipse An ellipse is represented by a centre, the direction of one semi-axis and the length of the two semi-axis. The plane in which the ellipse lies is required if the dimension of the geometry space is larger than 2. An ellipse is parameterized in terms of the angle which gives a bounded parameterization.
• Line A line is given by a point and a direction. It has an unbounded parameterization, $t \in [- \infty , \infty ]$.
• Parabola A parabola is given by a position, $C$, a focal distance, $F$, and a coordinate system, $({\bf x}, {\bf y}, {\bf z})$. It is described as $f(t) = C + F(t^2 {\bf x} + 2t{\bf y})$ and has an unbounded parameterization, $t \in [- \infty , \infty ]$.
• Hyperbola A hyperbola is given by a position, a coordinate system and two distances. The parameterization is unbounded.

Other Surface Types

Similar to the curve case, GoTools supports also other types of parametric surfaces than spline surfaces. The additional surface types are bounded surface, elementary surface and composite surface. The elementary surfaces are conic surfaces, plane and torus. A composite surface consists of a number of spline surfaces where the associated parameter domains are mapped into one composite domain. The class is not complete in the sense that it does not support all functions specified in the interface for a parametric surface.

Bounded Surface

A bounded surface is a trimmed surface defined by an underlying surface and a trimming loop. The underlying surface is a parametric surface and the loop consists of a closed sequence of ordered parametric curves, often of type CurveOnSurface. The trimming loop must lie on the surface and be continuous with respect to a given tolerance.

Elementary Surface

Also the ElementarySurface is quite new in GoTools, and it has been entered as an entity from IGES or STEP. The elementary surfaces may also be represented as spline surfaces although non-bounded surfaces must be given a finite extension. Operations involving this curve may, however, be made more efficiently by the knowledge of the surface type. The elementary surfaces is of the types:

• Cone A cone is described by a location, the cone axis, the radius of the cross section corresponding to the location and the cone angle. The parameterization is given by the angle and the distance along the axis, thus it is unbounded in one parameter direction.
• Cylinder A cylinder is given by its centre and radius and the cylinder axis. It is parameterized by the angle around the circle and the distance in the axis direction.
• Plane A plane is given by a point and a normal. It has an unbounded parameterization in both parameter directions.
• Sphere A sphere is given by its centre and radius. It has an angular parameterization in both parameter directions and thereby bounded.
• Torus A torus is given by the minor and major radius, a location and an axis. The parameterization is angular in both parameter directions.
• Disc A disc is a part of a plane limited by a circle and given by its centre, radius, plane normal and an additional vector to generate a coordinate system.

The elementary surfaces described above is placed in a coordinate system to facilitate the parameterization. In addition to the geometric information given for each entity, remaining coordinate system information must be specified.