Module TrivariateModel

The module trivariatemodel contains the representation format for a set of volumes and tools to act upon the VolumeModel.

The module depends on:

• gotools-core
• GoTools compositemodel
• GoTools trivariate
• Modules that compositemodel depends upon

Volume Topology

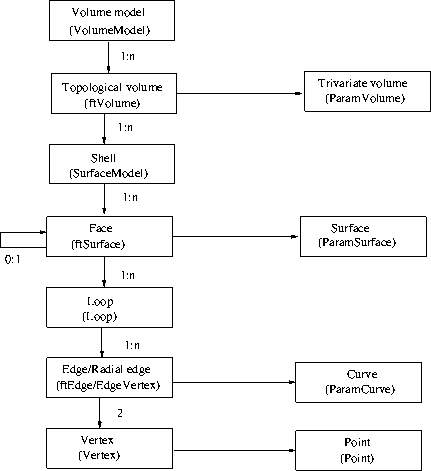
Topology structures for a volume model. The GoTools class names are given in brackets.

The volume topology in GoTools is an extension to the boundary-represented topology implemented in the module compositemodel. However, in contrast to the boundary-represented topology, the volume topology is not manifold. Thus, we can expect more than two faces to meet in an edge.

The top entity in the topology structure is the volume model (VolumeModel), which consists of a set of volumes. Each volume has a topological entity implemented in ftVolume and a geometrical representation implemented as a ParamVolume. Information about the geometric representation of a volume can be found in the module [[trivariate|Module trivariate]].

ftVolume inherits Body in compositemodel and is, as a Body, surrounded by one or more shells each represented as a SurfaceModel. A shell is a collection of faces of type ftSurface that have a geometric representation as a ParamSurface, which is described in the submodule [[gotools-core/geometry|Module Geometry]].

A face is limited by a number of loops of type Loop that are sequences of edges of type ftEdge. In this context, the face is used to represent adjacency between volumes. An edge is limited by two vertices of type Vertex.

Volume Model

The inheritance tree for a volume model

VolumeModel is a CompositeModel as illustrated in the figure above. As such it inherites a function interface, but some methods are not implemented. Thus, the class is incomplete, but not in the sense of being a topological entity.

VolumeModel has the following functionality:

• Fetch one entity in the set, either as a topological or geometric volume
• Evaluate the volume model given information about which entity to evaluate
• Compute the bounding box as a BoundingBox
• Add a new volume to the volume model
• Remove one volume from the volume model
• Check if all geometrical volumes are NURBS
• Fetch all vertices in the model
• Fetch all radial edges (EdgeVertex) in the model
• Fetch non-radial edges, i.e., edges that do not belong to at least two volumes
• Fetch all inner faces in the model
• Fetch all boundary faces in the model
• Check if the model has a corner-to-corner configuration
• Ensure that the model has a corner-to-corner configuration
• Ensure that adjacent spline volumes share common spline spaces at common boundaries
• Fetch the boundary of the volume model described as a number of SurfaceModels
• Divide the volume model into connected volume models

The constructor of the volume model requires a number of tolerances, namely gap, neighbour, kink and bend; see the module quality model. These tolerances are the same as the ones required for a composite model.

Topological Volume Entity

The topological volume entity is implemented in the class ftVolume and it inherits Body from the compositemodel module. The name ftVolume is choosen to be in line with ftSurface and ftEdge. Those entities have got their names for historical reasons; the prefix ft has no deeper meaning.

An ftVolume is a Body and therefore has access to its shells, i.e., boundaries, and one can check whether two ftVolumes are adjacent. An ftVolume can also

• Fetch the corresponding geometry volume
• Fetch the bounding box of this volume
• Fetch all adjacent ftVolumes
• Fetch all radial edges belonging to this volume or being common between this volume and another volume
• Fetch edges belonging only to the current volume
• Compute adjacency information between the current volume and another volume
• Return information about outer boundaries
• Get local information about correspondence of coefficients of two adjacent spline volumes
• Return the relation between the current volume and a given vertex

An ftVolume may be trimmed. That is, the boundary faces of the volume may limit the extent of the underlying parametric volume. In this context the following functionality applies:

• Check if the volume is hexahedral
• Approximate a hexahedral trimmed volume by one spline volume
• Split a trimmed volume into a set of hexahedral trimmed volumes

Note that the functionality related to trimmed volumes is under development and currently very unstable and limited.

Extensions to Face

The initial implementation of a face as one entity in a boundary representation solid was no longer sufficient when the entity should serve as part of the boundary of a volume belonging to a volume model. Some extensions turned out to be required. The face ftSurface has knowledge about the Body it belongs to, if any. It also has a pointer to a boundary face belonging to an adjacent body. This pointer is used in the context of a volume model. During the assembly of a volume model, information about coincident boundary faces of the ftVolumes are computed, and the pointer representing adjacency is set accordingly.

An ftSurface provides access to its twin and to the, at most, two bodies sharing the common face represented by this ftSurface.

When the ftSurface represents the boundary surface of an ftVolume, the corresponding parametric surface will be of type SurfaceOnVolume. This class is implemented in the module trivariate. A SurfaceOnVolume has knowledge about the spatial representation of the surface, the ParamVolume to which it belongs and the position of the surface in the parameter domain of the volume. Currently, a SurfaceOnVolume is constructed only as a boundary surface of a SplineVolume. It contains enough information to identify which volume boundary it represents and the orientation of the surface compared to this boundary.

Radial Edge

In a non-manifold model, more than two faces can meet in an edge, and thus the half edge representation implemented in ftEdge is not sufficient to hold the model. The radial edge, EdgeVertex, is an extension to the topology structures of the compositemodel module, and the class itself is placed in compositemodel. An EdgeVertex contains information of all pairs of half edges, ftEdge, meeting in an edge, and each ftEdge belonging to an EdgeVertex has access to this EdgeVertex.

An EdgeVertex instance is defined when adjacency between two ftSurfaces is found. Thus, at edges in an ftVolume where no adjacent ftVolume exists, no EdgeVertex instance will be defined. Then the edge is represented with a pair of ftEdge instances.

The EdgeVertex class is placed in the module compositemodel, but is used in connection with volume models. In addition to functionality related to topology build, the class has some access functionality:

• Fetch edges meeting in the radial edge, either uniquely defined, i.e., one instance for a pair or twins, or absolutely all edges.
• Fetch a specified edge
• Check if an ftEdge belongs to a radial edge
• Check if an ftEdge belongs to a radial edge and has no information about a corresponding ftEdge. In that case the corresponding surface does not belong to a volume.
• Fetch adjacent faces
• Fetch adjacent bodies