-
Notifications
You must be signed in to change notification settings - Fork 7
Distancia de Levenshtein
En la teoría de la información y ciencia de la computación , la distancia de Levenshtein, distancia de edición, o distancia entre palabras, es una cadena métrica para diferenciar 2 secuencias. En esencia la distancia de Levenshtein entre dos cadenas es igual al número de modificaciones de un solo carácter necesario para cambiar una palabra en otra, en si se define como el número mínimo de cambios necesarios para realizar dicha transformación, las operaciones de edición son: inserción, eliminación y sustitución de un simple carácter.
Matemáticamente, la distancia de levenshtein entre 2 cadenas 
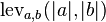
Note que el primer elemento mínimo corresponde a la eliminación desde a hasta b, el segundo a la inserción y el tercero para que coincida o no dependiendo de los símbolos del mismo.
La distancia de Levenshtein entre "casa" y "calle" es de 3 porque se necesitan al menos tres ediciones elementales para cambiar uno en el otro.
Casa → cala (sustitución de 's' por 'l')
cala → calla (inserción de 'l' entre 'l' y 'a')
calla → calle (sustitución de 'a' por 'e')
Se trata de un algoritmo de tipo bottom-up, común en programación dinámica. Se apoya en el uso de una matriz (n + 1) × (m + 1), donde n y m son las longitudes de los cadenas. Aquí se indica el algoritmo en pseudocódigo para una función LevenshteinDistance que toma dos cadenas, str1 de longitud lenStr1, y str2 de longitud lenStr2, y calcula la distancia Levenshtein entre ellos:
int LevenshteinDistance(char str1[1..lenStr1], char str2[1..lenStr2])
// d is a table with lenStr1+1 rows and lenStr2+1 columns
declare int d[0..lenStr1, 0..lenStr2]
// i and j are used to iterate over str1 and str2
declare int i, j, cost
for i from 0 to lenStr1
d[i, 0] := i
for j from 0 to lenStr2
d[0, j] := j
for i from 1 to lenStr1
for j from 1 to lenStr2
if str1[i] = str2[j] then cost := 0
else cost := 1
d[i, j] := minimum(
d[i-1, j] + 1, // deletion
d[i, j-1] + 1, // insertion
d[i-1, j-1] + cost // substitution
)
return d[lenStr1, lenStr2]
El invariante mantenido a través del algorítmo es que pueda transformar el segmento inicial str1[1..i] en str2[1..j] empleando un mínimo de d[i,j] operaciones. Al final, el elemento ubicado en la parte INFERIOR derecha de la matriz contiene la respuesta.## Uso de la distancia de Levenshtein El uso de este algoritmo es la base de los correctores ortográficos utilizados por Google, Office, Mozilla, etc.
Distancia de Levenshtein: http://es.wikipedia.org/wiki/Distancia_de_Levenshtein
Levenshtein Distance: http://en.wikipedia.org/wiki/Levenshtein_distance
