checkpoint_03

Flux from Uniformly Charged Rod

An infinitely long charged rod has uniform charge density of [\lambda], and passes through a cylinder (gray). The cylinder in case 2 has twice the radius and half the length compared to the cylinder in case 1.

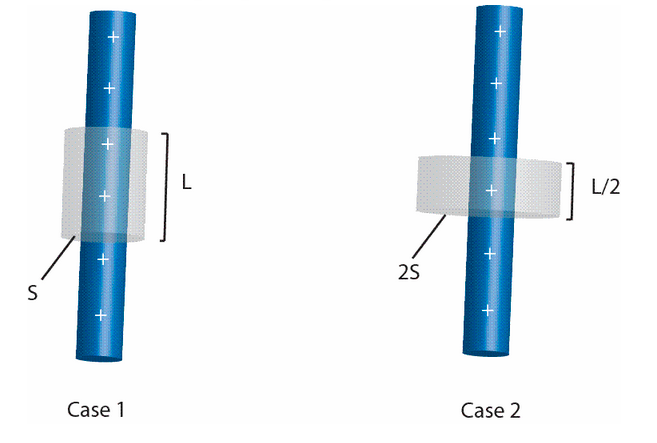
Compare the magnitude of the flux, [\phi], through the surface of the cylinder in both cases.

• [ \phi_1 = 2 \phi_2]
  • We are integrating over half the distance to compute the flux.

Flux from Point Charge Through Surfaces of Sphere

A positive charge (blue) is contained inside a spherical shell (black).

Consider two small surface elements on the shell surface [d_A] and [d_B], located on opposite side of the shell.

1)

How does the electric flux through the two surface elements, [d \phi_A] and [d \phi_B] change when the charge is moved from position 1 to position 2?

• [d \phi_A] increases and [d \phi_B] decreases.
  • The positive charge is closer to [d_A] in position 2.

2)

How does the flux [ \phi_E] through the entire surface change when the charge is moved from position 1 to position 2?

• Both [d \phi_A] and [d \phi_B] do not change.
  • The charge is still contained withing the surface in both cases.

Field Lines from Two Point Charges

The following three questions pertain to the electric field lines due to two c harges shown above.

1)

Compare the magnitudes of the two charges.

• [ |Q_1| > |Q_2| ]
  • Looking at the figure, more lines are protruding from charge [Q_1].

2)

What do we know about the signs of the charges from looking at the picture?

• [Q_1] and [Q_2] have opposite signs.
  • The electric field lines project directly from on charge to the other, indicating oposite signs.

3)

Compare the magnitudes of the electric fields at points [A] and [B].

• [ |E_A| < |E_B| ]
  • The filed at point [B] is more dense with electric field lines, indicating a higher magnitude than point [A].