checkpoint_06

Checkpoint 06

Spatial Dependence of Potential

The electric potential in a certain region is plotted in the following graph

1)

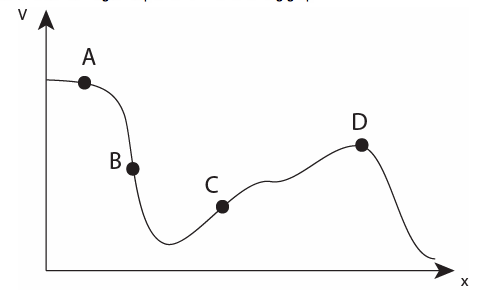
At which point is the magnitude of the [E]-field greatest?

• B
  • In order to maximize the [E]-field we are looking for the steepest slope or the point at which the electric potential is decreasing the fastest

2)

At which point is the direction of the [E]-field along the negative [x]-axis?

• C
  • The slope is increasing and therefore we are gaining potential energy.

Zero Electric Field

Suppose the electric field is zero in a certain region of space. Which of the following statements best describes the electric potential in this region?

• The electric potential is zero everywhere in this region.
• The electric potential is zero at at least one point in this region.
• The electric potential is constant everywhere in this region.
• There is not enough information given to distinguish which of the above answers is correct.
  • Only knowing that the electric field is zero in one point does not indicate to us enough information to say anything about the electric potential.

Electric Field Lines

The field-line representation of the [E]-field in a certain region in space is shown below. The dashed lines represent equipotential lines.

1)

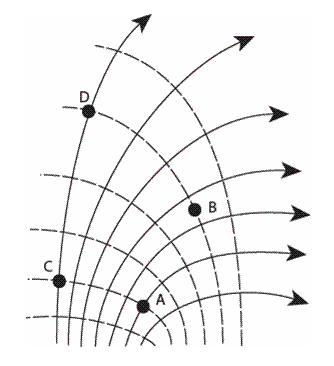
At which point in space is the [E]-field the weakest?

• [D]
  • At point [D] the field lines are most sparse.

2)

Compare the work done moving a negative charge from [A] to [B] and from [C] to [D]. Which one requires more work?

• More work is required to move a negative charge from [A] to [B] than from [C] to [D]
  • Based on the number of intersections of field lines, it is indicated that a greater "distance" exists between [A] and [B].
• More work is required to move a negative charge from [C] to [D] than from [A] to [B]
• The same amount of work is required to move a negative charge from [A] to [B] as to move it from [C] to [D]
• Cannot determine without performing the calculation

3)

Compare the work done moving a negative charge from [A] to [B] and from [A] to [D]. Which one requires more work?

• More work is required to move a negative charge from [A] to [B] than from [A] to [D]
• More work is required to move a negative charge from [A] to [D] than from [A] to [B]
  • The "distance" created by the field is greater from [A] to [D] vs [A] to [B]
• The same amount of work is required to move a negative charge from [A] to [B] as to move it from [A] to [D]
• Cannot determine without performing the calculation