Skip to content

prelecture_05_electric_potential_energy

Jump to bottom Edit New page
Kurt Robert Rudolph edited this page Jun 19, 2012 · 1 revision

Electric Potential Energy

Overview

  • Coulomb Force
    • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r}]
    • The work done by the Coulomb Force is independent from the path between those two points
    • A conservative force.

Work Done by Coulomb Force

  • [W_{AB} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left( \frac{ 1}{ r_A} - \frac{ 1}{ r_B}\right)]
    • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2} \hat r]
    • [W_{A \rightarrow B} = \int\limits_{r_A}^{r_B}{ \vec F_E \cdot d \vec r}]
      • [\vec F_E] and [d \vec r] are always in the same direction.
    • [W_{A \rightarrow B} = \int\limits_{r_A}^{r_B}{ F_E \cdot d r}]
    • [W_{A \rightarrow B} = \int\limits_{r_A}^{r_B}{ \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2} d r}]
    • [W_{A \rightarrow B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \int\limits_{r_A}^{r_B}{ \frac{ 1}{ r^2} d r}]
    • [W_{A \rightarrow B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left[-\frac{ 1}{ r} \right]\limits_{r_A}^{r_B}]
    • [W_{A \rightarrow B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r_A} - \frac{ 1}{ r_B}\right)]

Question 1

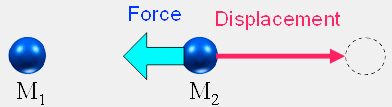
Masses [M_1] and [M_2] are initially separated by a distance [R_a]. Mass [M_2] is now moved further away from mass [M_1] such that their final separation is [R_b].

Which of the following statements best describes the work [W_{ab}] done by the force of gravity on [M_2] as it moves from [R_a] to [R_b]?

  • [W_{ab} < 0]
    • Since the gravitational force on [M_2] and the displacement of [M_2] are in the opposite direction, the work done by the force of gravity as [M_2] moves is negative.

Coulomb Force is a Conservative Force

  • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r}]
  • [W_{AB} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left( \frac{ 1}{ r_A} - \frac{ 1}{ r_B}\right)]

Electric Potential Energy

  • [U_r \equiv \Delta U_{\infty r} = \frac{ Q q}{ 4 \pi \varepsilon r}]
    • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r}]
    • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r} \rightarrow U]
    • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r} \rightarrow \Delta U = -W]
    • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r} \rightarrow \Delta U_{A B} = -\frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r_A} + \frac{ 1}{ r_B}\right)]
    • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r} \rightarrow \Delta U_{A B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(-\frac{ 1}{ r_A} + \frac{ 1}{ r_B}\right)]
    • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r} \rightarrow \Delta U_{A B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r_B} - \frac{ 1}{ r_A}\right)]
    • Change in Potential Energy:
      • [\Delta U_{A B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r_B} - \frac{ 1}{ r_A}\right)]
      • [\Delta U_{r_0 B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r_B} - \frac{ 1}{ r_0}\right)]
      • [\Delta U_{\infty B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r_B} - \frac{ 1}{ \infty}\right)]
        • Since were dealing with point charges aparently it's natural to let [r_0] to be infinity (i.e. magic).
      • [\Delta U_{\infty B} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r_B}\right)]
      • [\Delta U_{\infty r} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r}\right)]
      • [U_r \equiv \Delta U_{\infty r} = \frac{ Q q}{ 4 \pi \varepsilon_0} \left(\frac{ 1}{ r}\right)]
      • [U_r \equiv \Delta U_{\infty r} = \frac{ Q q}{ 4 \pi \varepsilon r}]

Question 2

n Case A two charges which are equal in magnitude but opposite in charge are separated by a distance [d]. In Case B the same charges are separated by a distance [2d].

Which configuration has the highest potential energy [U]?

  • Case B has the highest potential energy
    • The plot of [U(r)] shown below helps illustrate why this answer is correct. As the separation of the charges is increased we move to the right along the blue plot shown. Since the plot is going upward as we move to the right, U is increasing with separation.

Example: Calculated Speed

  • Let

    • [q_1, q_2] be two point charges
    • [v] be th velocity of [q_2].
    • [d] be the destance we begin our calculation
    • the distance where the [v] is desired to be known

  • [v = \sqrt{ \frac{ q_1 q_2}{ 2 \pi \varepsilon_0 m_2} \left(\frac{ 1}{ d} - \frac{ 1}{ x}\right)}]

    • [E_{Mechanical} = Constant]
    • [E_{Mechanical} = K + U]
    • [K_{initial} + U_{initial} = K_{final} + U_{final}]
    • [U_{initial} = K_{final} + U_{final}]
      • [K_{initial} = 0]
    • [U_{initial} - U_{final} = K_{final}]
    • [U_{initial} - U_{final} = \frac{ 1}{ 2} m_2 v^2]
    • [\frac{ q_1 q_2}{ 4 \pi \epsilon_0} \left(\frac{ 1}{ d} - \frac{ 1}{ x}\right) = \frac{ 1}{ 2} m_2 v^2]
    • [\frac{ q_1 q_2}{ 2 \pi \epsilon_0} \left(\frac{ 1}{ d} - \frac{ 1}{ x}\right) = m_2 v^2]
    • [\frac{ q_1 q_2}{ 2 \pi \epsilon_0 m_2} \left(\frac{ 1}{ d} - \frac{ 1}{ x}\right) = v^2]
    • [\sqrt{\frac{ q_1 q_2}{ 2 \pi \epsilon_0 m_2} \left(\frac{ 1}{ d} - \frac{ 1}{ x}\right)} = v]
    • [v = \sqrt{ \frac{ q_1 q_2}{ 2 \pi \varepsilon_0 m_2} \left(\frac{ 1}{ d} - \frac{ 1}{ x}\right)}]

Example: System of Three Particles

  • [U_{System} = k \sum\limits_{pairs}{ \frac{ q_i q_j}{ r_{ij}}}]
    • Let
      • [q_1,q_2,q_3] be point charges
      • [r_{1,2} = d, r_{1,3} = d, r_{2,3} = d]
    • Then
      • [U_{System} = \Delta U_1 + \Delta U_2 + \Delta U_3]
      • [U_{System} = \Delta U_1 + \Delta U_2 + \Delta U_3]
        • Bring each of the chages in from infinity
          • [U_{System} = 0] * [\Delta U_1 = 0]
          • [U_{System} = k \frac{ q_1 q_2}{ d}] * [\Delta U_2 = k \frac{ q_1 q_2}{ d}]
          • [U_{System} = k \frac{ q_1 q_2}{ d}] * [\Delta U_3 = k \frac{ q_1 q_3}{ d} + k \frac{ q_2 q_3}{ d}]
          • [U_{System} = k \frac{ q_1 q_2}{ d} + k \frac{ q_1 q_3}{ d} + k \frac{ q_2 q_3}{ d}]

Question 3

Two positive charges and one negative charge, all having magnitude [Q] are arranged at the vertices of an equilateral triangle as shown.

Three students are trying to determine the sign of the potential energy of this collection of charges, and they come up with the three answers shown below.

Which of their arguments is correct?

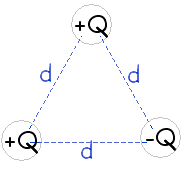
  • The potential energy of the system of charges is negative because it is calculated from the sum of two negative terms and one positive term.
    • The potential energy of a system of charges is defined to be the negative of the work done by the electric force in assembling the charges from infinity, one by one. It costs nothing to bring the first charge (let's say the bottom positive charge) into its place. Positive work is done by the electric force in bringing the bottom negative charge into its place. Negative work is done bringing the top positive charge into its place due to the field produced by the bottom positive charge. Positive work is done bringing the top positive charge into its place due to the field produced by the bottom negative charge. The magnitudes of each of these works are the same since the charges are all equidistant. Consequently the work done by the electric force in assembling these charges is positive (2 positive terms and one negative term, all having the same magnitude). Therefore the potential energy of the system is negaitve (2 negative terms and one positive term).

Summary: The Main Ideas

  • [\vec F_E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ Q q}{ r^2}\hat{ r} \Rightarrow \Delta U = -\int\limits_{A \rightarrow B}{ q \vec E \cdot d \vec l}]
    • Coulomb Force [\rightarrow] Conservation Force [\rightarrow] Potential Energy
  • Electric Potential Energy
    • Pair of Charged Particles
      • [U(r) = \frac{ Q q}{ 4 \pi \varepsilon_0 r}]
    • System of [N] Charged Particles
Add a custom footer
Add a custom sidebar
Clone this wiki locally