prelecture_12_magnetism

Magnetism

Overview

• start wit observations about
  • bar magnets
  • compass needles
  • current caring wires
• Well see that magnetic effects can be described by another vector field, appropriately name the magnetic field, that is created by electric charges in motion.
• First will we asses the forces magnetic fields have on charged particles.
  • Larentz Force [\vec F = q \vec E + q \vec v \times \vec B]
    • The general equation which describes the force on a charged particle as it moves through regions containing electric and magnetic fields.
• We finish by examining a few examples.

Magnetic Observations

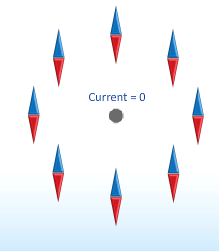
• Bar Magnet
  • 
  • the ends are usually called the Nort and South poles
  • opposite poles attract
  • like poles repel
  • filed around a bar magnet is similar to an electric dipole
    • 
    • note the triangles in the field represent compass needles small bar magnets able to piviot about their central axis and align with the field in their proximity
  • if a bar magnet is cut in half you end up with two bar magnets, not isolated north and south poles.
    • 

Question 1

We have just discussed what most of you have known since elementary school - that the north pole of one magnet is attracted to the south pole of another magnet. We also know that the needle of a compass is itself a magnet. In view of this, how can we explain that the north pole of a compass needle seems to be attracted to the north pole of the planet Earth?

• The geographic North pole of the earth is actually the South magnetic pole of the Earth.

Source of Magnetic Field

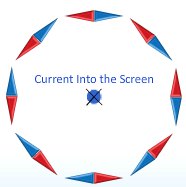
• Electric Currents create magnetic fields
  • 
  • 
  • 
• all electric fields are created by charges in motion.
• Passing a current through a wire produces magnetic field and you see according forces between them
  • 
    • same direction produces attractive force
  • 
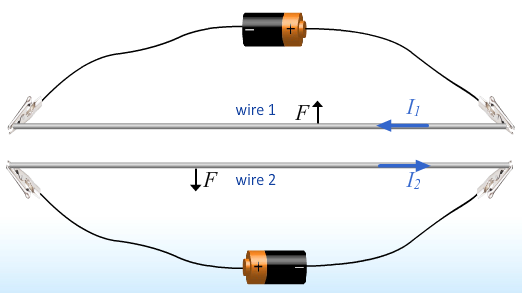
    • opposite direction produces repulsive force

Magnetic Force

• Just saw two wires create an electric force on one another
• We find that the magnetic field around a wire is always perpendicular to the wire and in a clockwise or counter clockwise direction.
  • 
• This indicates to us that
  • Force is perpendicular to current
    • [\vec F \perp \vec I] and [\vec F \perp \vec B]
      • Both to the direction of the current and the direction of the magnetic field.
  • Cross product is a good mathematical model for this
    • 
    • [\vec F = q \vec v \times \vec B]

Cross Products

• [|\vec A \times \vec B| = A B \sin \theta]
• Right Hand Rules
  • Version 1
    • Fingers point in direction of [\vec A]
    • Curl fingers toward [\vec B]
    • Thumb gives direction of [\vec A \times \vec B]
  • Version 2
    • Point thumb in direction of [\vec A]
    • Point fingers in direction of [\vec B]
    • Palm gives direction of [\vec A \times \vec B]

Question 2

The picture below shows a cathode ray tube in a magnetic field. A beam of electrons is produced at the cathode and travels with a high velocity toward a fluorescent screen. In the absence of a magnetic field the beam of electrons would hit the screen at the center (labeled 2 in the picture). When the orientation of the magnetic field is in the [-y] direction as shown, at which of the points on the screen would the beam arrive?

• [1]
  • Taking the cross product between the velocity of the electrons ([+z] direction) and the magnetic field ([-y] direction) results in a vector pointing in the [+x] direction. Since the charge of the electrons are negative, however, we have to factor in another minus sign, which makes the resulting force point in the [-x] direction. The beam will therefore strike at the point labeled [1].

Velocity Selector

• 
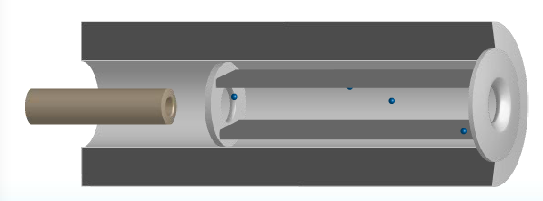
  • A device oriented with a long narrow channel ensuring that all particles exiting the tube are traveling in the same direction.
  • As well, the device employs a electric and magnetic fields throughout the channel in order to ensure the particles are traveling at the same speed.
    • Orient the fields such that [\vec F_{Electric} = -\vec F_{Magnetic}]
    • [q \vec E = - q \vec v \times \vec B] * only particle with that unique speed will now exit the channel * particles with all other speeds will be deflectd by the non-zero combination of the electric and magnetic forces
    • [v = \frac{ E}{ B}] when [\vec F_B = -\vec F_B]

Motion in an Uniform B Field

• 
  • Force on th particle is the magnetic force [\vec F_B = q \vec v \times \vec B]
  • suppose the force of the magnetic field is perpendicular to the velocity
    • [F_B = q v B]
    • This gives rise to a centripetal acceleration of constant magnitude [a_c = \frac{ v^2}{ R}]
    • 
    • which gives us [\frac{ q v B}{ m} = \frac{ v^2}{ R}]
    • hence [R = \frac{ m v}{ q B}] the radius of the circle

Question 3

Particle [A] has twice the charge and [4] times the mass of particle [B]. Suppose [A] and [B] have the same kinetic energy [K] and move perpendicular to a constant magnetic field. Which partilce moves in the smallest circle? (It may help you to recall that [K] can be expressed as \frac{ p^2}{ 2m}.)

• Particles [A] and [B] move in circles of the same radius
  • [R^2 = \frac{ 2 m k}{ (q B)^2}]
  • Doubling the charge [q] and quadrupling the mass [m] leaves [R] unchanged since both the numerator and denominator increase by [4].

Summary: The Main Ideas

• Introduces observations involving forces exerted by bar magnets, and current carrying wires to indicate the existence of magnetic fields.
  • summary.png
• All magnetic effects are able to be described in terms of magnetic field that is created by the motion of charged particles
• These magnetic fields create forces on electric charges that are in motion. We introduced the magnetic form for this in terms of the cross product of vectors.
  • [\vec F = q \vec v \times \vec B]