prelecture_15_amperes_law

Ampere's Law

Overview

• Last time, Biot-Savart Law which allows us to calculate the magnetic field produced by an arbitrary current distribution.
• Now, Ampere's Law which defines the integral within a closed path to a current passing through the area of that path
  • [\oint\limits_{loop} \vec B \cdot d \vec l = \mu_0 I_{enclosed}]
  • 

Review of Gauss' Law

• Recall we represented an electric field by a point charge by a set of radial field lines emanating from the charge with the number of these lines being proportional to the magnitude of this field
  • 
• Electric Flux through any surface
  • [\Sigma_E \equiv \int\limits_{surface} \vec E \cdot d \vec A]
  • 
• Gauss' Law
  • [\oint\limits_{surface} \vec E \cdot d \vec A = \frac{ q_enclosed}{ \varepsilon_0}]

Motivating Ampere's Law

• Ampere's Law
  • [\oint\limits_{loop} \vec B \cdot d \vec l = \mu_0 I]
  • Holds true of any path which current flows through
  • 

Question 1

A current [I] flow in a long straight wire as shown. In Case 1 we consider [\oint\limits_{loop} \vec B \cdot d \vec l] along a circular path of radius [R] centered on the wire, and in Case 2 we consider [\oint\limits_{loop} \vec B \cdot d \vec l] along a circular path of radius [2R] centered on the wire:

How do the magnitudes of [\oint\limits_{loop} \vec B \cdot d \vec l] around the closed paths compare?

• They are the same
  • As shown in the following diagram, the strength of the magnetic field [B] is reduced by a factor of two since it scales like [\frac{ 1}{ R}], and the length of the path [L] increases by a factor of two since the circumference of a circle scales like [R] i.e., [C = 2 \pi R]. These two factors cancel, and the net effect is that the [\oint\limits_{loop} \vec B \cdot d \vec l] around the closed path does not depend on the radius of the circle at all:
    • 

Example: Integrating with Semicircles

• Consider magnetic field produced by an infinite strait wire carrying current [I],
  • [\oint\limits_{loop} \vec B \cdot d \vec l]
  • we will consider a path connecting two semicircles.
    • 
  • Consider the integral between four points [a, b, c, d]
    • 
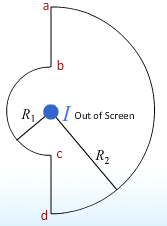
    • [\oint\limits_{loop} \vec B \cdot d \vec l = \oint\limits_{a}^{b} \vec B \cdot d \vec l
      • \oint\limits_{b}^{c} \vec B \cdot d \vec l
      • \oint\limits_{c}^{d} \vec B \cdot d \vec l
      • \oint\limits_{d}^{a} \vec B \cdot d \vec l] [= \oint\limits_{b}^{c} \vec B \cdot d \vec l
      • \oint\limits_{d}^{a} \vec B \cdot d \vec l]
        • [\oint\limits_{b}^{c} \vec B \cdot d \vec l = B( \pi R_{ba}) = \frac{ \mu_0 I}{ 2 \pi R_{bc}} (\pi R_{bc}) = \frac{ \mu_0 I}{ 2}] * [B_{ba} = \frac{ \mu_0 I}{ 2 \pi R_ba}]
        • [\oint\limits_{d}^{a} \vec B \cdot d \vec l = \frac{ \mu_0 I}{ 2}]
    • [\oint\limits_{loop} \vec B \cdot d \vec l = \mu_0 I] * Note that this is identical to a perfectly circular path.

Example: Integrating with Semicircles II

• Consider magnetic field produced by an infinite strait wire carrying current [I],
  • flip the path so it no longer contains the current carrying wire
    • 
  • [\oint\limits_{loop} \vec B \cdot d \vec l = 0 ]

Ampere's Law

• The result of Ampere's Law is general
  • [\oint\limits_{loop} \vec B \cdot d \vec l = \mu_0 I_{enclosed} ]

Question 2

A long straight wire (the red dot in the diagram below) carries current [I] directly out of the plane of the page. Consider the two closed integration paths shown in Case 1 and Case 2:

How do the magnitudes of the [\oint\limits_{loop} \vec B \cdot d \vec l] around the closed paths compare?

• It is the same in both cases
  • This is easily seen by shading in the areas enclosed by the closed paths in both cases:
    • 
  • Since neither path encloses any current, neither can have a non-zero [\oint\limits_{loop} \vec B \cdot d \vec l].

Magnetic Field Inside of a Wire

[\oint\limits_{loop} \vec B \cdot d \vec l = B\oint\limits_{loop} d l = B (2 \pi r)]

[= \mu_0 I_{enclosed} = \mu_0 I \frac{ \pi r^2}{ \pi a^2}]

Hence

[B = \frac{ \mu_0 I}{ 2 \pi a^2} r] for [ r < a]

[B = \frac{ \mu_0 I}{ 2 \pi r}] for [ r > a]

Magnetic Field and Infinite Sheet of Current

• [B = \frac{ 1}{ 2} \mu_0 n I]
  • [n \equiv \frac{ number_of_wires}{ unit_length}