Skip to content

prelecture_06_electric_potential

Jump to bottom Edit New page
Kurt Robert Rudolph edited this page Jun 20, 2012 · 2 revisions

Electric Potential

Overview

  • Electric Potential Energy
    • [U \propto q]
    • Electric potential energy is proportional to it's charge.
    • Hence we are able to define a new quantity Electric Potential
  • Electric Potential
    • [V \equiv \frac{ U}{ q}]
    • Similar to Electric Field
      • [\vec E \equiv \frac{ \vec F_{Coulomb}}{ q}]

Electric Potential V

  • Electric Potential Energy
    • [U \propto q]
  • Electric Potential Difference
    • [\Delta V \equiv \frac{ \Delta U}{ q}]
      • The change in electric potential energy per unit charge
      • [W_{A \rightarrow B} = \int\limits_{A}^{B}{ \vec F \cdot d \vec l}]
        • Electric Potential Energy
      • [W_{A \rightarrow B} = \int\limits_{A}^{B}{ q \vec E \cdot d \vec l}]
        • We can express the Coloumb force at at any point along the path from [A] to [B] as the product of the charge and the electric field.
      • [\Delta U_{A \rightarrow B} = -\int\limits_{A}^{B}{ q \vec E \cdot d \vec l}]
        • [\Delta U_{A \rightarrow B} = -[W_{A \rightarrow B}]
      • [\Delta U_{A \rightarrow B} = -q \int\limits_{A}^{B}{ \vec E \cdot d \vec l}]
        • Note that the change in potential energy is proportional to the charge [q]
      • Therefore [\Delta V_{A \rightarrow B} \equiv \frac{ \Delta U_{A \rightarrow B}}{ q} = -\int\limits_{A}^{B}{ \vec E \cdot d \vec l}]

  • Electric potential difference

    • [\Delta V_{A \rightarrow B} \equiv \frac{ \Delta U_{A \rightarrow B}}{ q} = -\int\limits_{A}^{B}{ \vec E \cdot d \vec l}]

  • Electric Field

    • [\vec E = k \frac{ Q}{ r^2} \hat r]

  • [\Delta V_{A \rightarrow B} = -\int\limits_{A}^{B}{ \vec E \cdot d \vec l}]

  • [\Delta V_{A \rightarrow B} = -\int\limits_{A}^{B}{ k \frac{ Q}{ r^2} \hat r \cdot d \vec r}]

  • [\Delta V_{A \rightarrow B} = k Q \left(\frac{ 1}{ r_B} - \frac{ 1}{ r_A}\right)]

    • The electric potential difference is proportional to inverse distances from the point charge.

  • [V( r) = \fra{ k Q}{ r}]

    • When we let [r_0 = \infty]
    • [V( r) \equiv \Delta V_{r_0 \rightarrow r} = k Q \left(\frac{ 1}{ r} - \frac{ 1}{ r_0}\right)]
      • It is common to introduce a quantity [V( r)] which is defined for each single point in space

  • SI Units are [V = \frac{ J}{ C}] or volts equals joules per coulomb

E from V

  • We just defined Electric Potential [V( r) = -\int\limits_{_r_0}^{r}{ \vec E \cdot d \vec r}]
  • We are able to take the derivative of the electric potential to determine the electic fieled
    • [\vec E( r) = -\frac{ dv}{ dr} \hat r]

Example

  • [V( r) = k \frac{ Q}{ r}]
  • [E = -\frac{ dV}{ dr}]
  • [E = -\frac{ d}{ dr} \left( k \frac{ Q}{ r}\right)]
  • [E = -\left(-k \frac{ Q}{ r^}\right)]
  • [E = k \frac{ Q}{ r^}]

In Multiple Dimensions...

  • [\vec \nabla V = \frac{ \partial V}{ \partial x} \hat i + \frac{ \patial V}{ \partial y} \hat j + \frac{ \partial V}{ \partial z} \hat k]
    • [\vec \nabla V] is the gradient of potential
  • The Gradient in Different Coordinate Systems
    • Cartesian [\vec \nabla V = \frac{ \partial V}{ \partial x} \hat i + \frac{ \partial V}{ \partial y} \hat j + \frac{ \partial V}{ \partial z} \hat k]
    • Spherical [\vec \nabla V = \frac{ \partial V}{ \partial r} \hat r + \frac{ 1}{ r} \frac{ \partial V}{ \partial \theta} \hat \theta + \frac{ 1}{ r \sin \theta} \frac{ \partial V}{ \partial \phi} \hat \phi]
    • Cylindrical [\vec \nabla V = \frac{ \partial V}{ \partial r} \hat r + \frac{ 1}{ r} \frac{ \partial V}{ \partial \theta} \hat \theta + \frac{ \partial V}{ \partial k} \hat k]

Equipotentials

  • [V_{Total} = \sum\limits_{i}{ V_i}]

Question 1

A system made up of a positive charge and a negative charge has the equipotentials shown below. The difference in potential between adjacent lines is the same (just like the lines of constant altitude on a topographical map.)

Compare the magnitudes of the two charges.

  • The magnitude of the positive charge is greater than the magnitude of the negative charge.

Example: Discrete Charges

  • [V_P = \sum\limits_{i}{ V_i}]
  • [V_P = V_1 + V_2 + V_3]
  • [V_P = k \frac{ Q_1}{ r_1} + k \frac{ Q_2}{ r_2} + k \frac{ Q_3}{ r_3}]
  • [V_P = k \frac{ q}{ a} + k \frac{ -q}{ a \sqrt{ 2}} + k \frac{ q}{ a}]
  • [V_P = k \frac{ q}{ a} \left(2 - \frac{ \sqrt{ 2}}{ 2}\right)]

Question 2

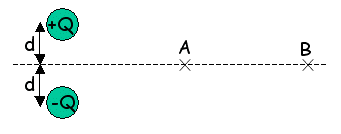
An electric dipole with charge magnitude [Q] and separation [2d] is oriented as shown below. Compare [V_A], the electric potential at point [A], with [V_B], the electric potential at point [B].

  • [ V_A = V_B]
    • [V_{B A} = -\int\limits_{A}^{B}{ \vec E \cdot d \vec L]
    • The electric field at any point is the vector sum of the electric fields produced by the positive charge [(E+)] and the negative charge [(E−)]. The symmetry of the charges about the dashed line going through [A] and [B] means that the horizontal electric field components of [E+] and [E−] will cancel at any point on this line, as shown below:

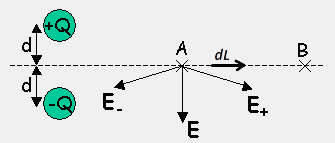
  • The net electric field along this line is therefore perpendicular to this line, hence the dot product of [\vec E] and [d \vec L] is zero everywhere along this line. According to the above equation, this means that the potential anywhere on the line is the same.

Example: Charged Spherical Insulator

  • Recall Electric Field for a solid insulator
    • [r < a]
      • [E = k \frac{ Q}{ a^3} r]
    • [r > a]
      • [E = k \frac{ Q}{ r^2}]
  • Finding Electric Potential
    • [V( r) \equiv \Delta V_{\infty \rightarrow r} = -\int\limits_{\infty}^{r}{ \vec E \cdot d \vec l}]
    • [V( r) = -\int\limits_{\infty}^{r}{ \vec E \cdot d \vec l}]
    • [r > a]
      • [V( r) = -\int\limits_{\infty}^{r}{ k \frac{ Q}{ r^2} \hat r \cdot d \hat r]
      • [V( r) = k \frac{ Q}{ r}]
    • [r < a]
      • [V( r) = -\int\limits_{\infty}^{r}{ \vec E \cdot d \vec l}]
      • [V( r) = -\int\limits_{\infty}^{a}{ \vec E \cdot d \vec l} - \int\limits_{a}^{r}{ \vec E \cdot d \vec l}]
      • [V( r) = -\int\limits_{\infty}^{a}{ E \cdot d r} - \int\limits_{a}^{r}{ E \cdot d r}]
        • in both integral regions [E] is parallel to [r]
      • [V( r) = -\int\limits_{\infty}^{a}{ k \frac{ Q}{ r^2} dr } - \int\limits_{a}^{r}{ k \frac{ Q}{ a^3} r d r}]
      • [V( r) = k \frac{ Q}{ a} + k \frac{ Q}{ 2 a^3} (a^2 - r^2)]
      • [V( r) = k \frac{ Q}{ 2 a^3} (3 a^2 - r^2)]

Question 3

Which of the following equipotential diagrams best describes the spherical insulator in the previous example? (The colored circle in the center represents the insulator.)

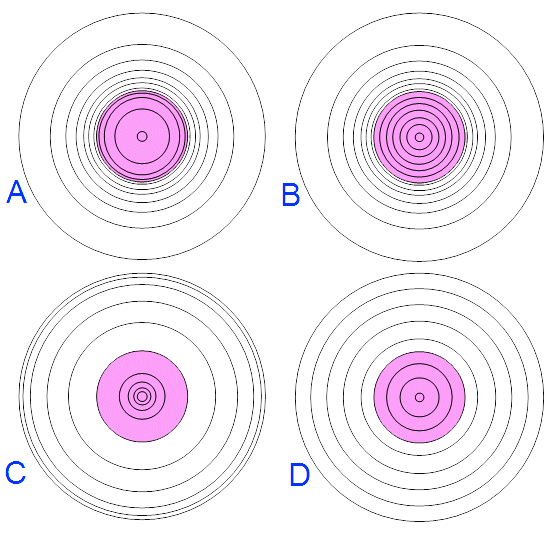
  • A
    • The separation of the equipotentials is smallest at the outer radius of the pink sphere since the electric field is strongest there. The separation of the equipotentials increases where the electric field is weaker; both toward the center of the sphere and far away from the sphere.

The Big Picture

  • Coulomb Force [\vec F = k \frac{ Q q}{ r^2} \hat r]
    • [\vec F = q k \frac{ Q}{ r^2} \hat r]
    • [\frac{ \vec F}{ q} = k \frac{ Q}{ r^2} \hat r]
    • [\vec E_Q \equiv \frac{ \vec F}{ q} = k \frac{ Q}{ r^2} \hat r]
  • Electric Field
    • [\vec E_Q \equiv \frac{ \vec F}{ q}]
      • Vector
  • Electric Potential
    • [V_Q \equiv \frac{ U}{ q}]
      • Scalar

Summary

  • Electric Potential
    • [V( r)]
    • [V( \vec r) \equiv \Delta V_{\hat r_0 \rightarrow \vec r} = -\int\limits_{\hat r_0}^{\hat r}{ \vec E \cdot d \vec l}] * where [V( \vec r_0) \equiv 0]
  • Electric Potential Difference
    • [\Delta V_{A \rightarrow B} \equiv \frac{ \Delta U_{A \rightarrow B}}{ q}]
    • [\Delta V_{A \rightarrow B} = - \int\limits_{A}^{B}{ \vec E \cdot d \vec l}]
  • Electric Field can be obtained by applying the gradiend function
    • [\vec E = - \vec \nabla V]
Add a custom footer
Add a custom sidebar
Clone this wiki locally