-
Notifications
You must be signed in to change notification settings - Fork 52
homework_01_point_charges_in_two_dimensions
Kurt Robert Rudolph edited this page Jun 13, 2012
·
16 revisions
Three charges ([q_1 = 5.9 \mu C, q_2 = -4.3 \mu C, and q_3 = 3.6 \muC]) are located at the vertices of an equilateral triangle with side [d = 9.5 cm] as shown.
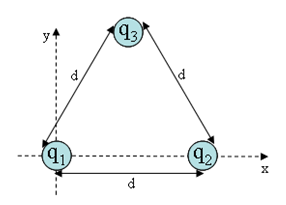
What is [F_{3,x}], the value of the [x]-component of the net force on [q_3]?
- [F_{ij} = \kappa \frac{ q_i q_j}{ r^2} \hat r]
- [ \kappa = \frac{ 1}{ 4 \pi \epsilon_0} = 8.99 \times 10^9 \frac{ Nm^2}{ C^2} ]
- [ \mu = 10^{-6}]
- Let:
- [ i = q_1 = 5.9 \mu C]
- [ j = q_2 = -4.3 \mu C ]
- [ k = q_3 = 3.6 \mu C ]
- [ d = 0.095 m ]
- [ \theta = 60 ]
- [ F_{k,x} = \kappa \frac{ q_i q_k}{ d^2} \cos{ \left( \theta \right)} +\kappa \frac{ q_j q_k}{ d^2} \cos{ \left( \theta \right)} = 18.2888 N]
What is [F_{3,y}], the value of the [y]-component of the net force on [q_3]?
- [F_{ij} = \kappa \frac{ q_i q_j}{ r^2} \hat r]
- [ \kappa = \frac{ 1}{ 4 \pi \epsilon_0} = 8.99 \times 10^9 \frac{ Nm^2}{ C^2} ]
- [ \mu = 10^{-6}]
- Let:
- [ i = q_1 = 5.9 \mu C]
- [ j = q_2 = -4.3 \mu C ]
- [ k = q_3 = 3.6 \mu C ]
- [ d = 0.095 m ]
- [ \theta = 60 ]
- [ F_{k,y} = \kappa \frac{ q_i q_k}{ d^2} \sin{ \left( \theta \right)} - \kappa \frac{ q_j q_k}{ d^2} \sin{ \left( \theta \right)} = 4.96896 N]

A charge [q_4 = 3.6 \mu C] is now added as shown.
What is [F_{2,x}], the [x]-component of the new net force on [q_2]?
- [F_{ij} = \kappa \frac{ q_i q_j}{ r^2} \hat r]
- [ \kappa = \frac{ 1}{ 4 \pi \epsilon_0} = 8.99 \times 10^9 \frac{ Nm^2}{ C^2} ]
- [ \mu = 10^{-6}]
- Let:
- [ i = q_1 = 5.9 \mu C]
- [ j = q_2 = -4.3 \mu C ]
- [ k = q_3 = q_4 3.6 \mu C ]
- [ d = 0.095 m ]
- [ a = \left( \frac{ d}{ 2} \right) = .0475 m]
- [ b = \sqrt{d^2 - a^2} = .0822]
- [ \theta = \arctan{ \left( \frac{ a}{ b} \right)} = 30 ]
- [ F_{j,x} = \kappa \frac{ q_i q_j}{ d^2} +2\left( \kappa \frac{ q_k q_j}{ d^2} \sin{ \left( \theta \right)} \right) = -40.6916 N]
What is [F_{2,y}], the [y]-component of the new net force on [q_2]?
- [F_{ij} = \kappa \frac{ q_i q_j}{ r^2} \hat r]
- [ \kappa = \frac{ 1}{ 4 \pi \epsilon_0} = 8.99 \times 10^9 \frac{ Nm^2}{ C^2} ]
- [ \mu = 10^{-6}]
- Let:
- [ i = q_1 = 5.9 \mu C]
- [ j = q_2 = -4.3 \mu C ]
- [ k = q_3 = q_4 3.6 \mu C ]
- [ d = 0.095 m ]
- [ a = \left( \frac{ d}{ 2} \right) = .0475 m]
- [ b = \sqrt{d^2 - a^2} = .0822]
- [ \theta = \arctan{ \left( \frac{ a}{ b} \right)} = 30 ]
- [F_{j,y} = 0 ]
What is [F_{1,x}], the [x]-component of the new net force on [q_1]?
- [F_{ij} = \kappa \frac{ q_i q_j}{ r^2} \hat r]
- [ \kappa = \frac{ 1}{ 4 \pi \epsilon_0} = 8.99 \times 10^9 \frac{ Nm^2}{ C^2} ]
- [ \mu = 10^{-6}]
- Let:
- [ i = q_1 = 5.9 \mu C]
- [ j = q_2 = -4.3 \mu C ]
- [ k = q_3 = q_4 3.6 \mu C ]
- [ d = 0.095 m ]
- [ a = \left( \frac{ d}{ 2} \right) = .0475 m]
- [ b = \sqrt{d^2 - a^2} = .0822]
- [ \theta = \arctan{ \left( \frac{ a}{ b} \right)} = 30 ]
- [ F_{i,x} = \kappa \frac{ q_j q_i}{ d^2} +2\left( \kappa \frac{ q_k q_i}{ d^2} \sin{ \left( \theta \right)} \right) = 46.4292 N]
How would you change [q_1] (keeping [q_2], [q_3] and [q_4] fixed) in order to make the net force on [q_2] equal to zero?
- Decrease its magnitude and change its sign.
- Let:
- [ i = q_1 = 5.9 \mu C]
- [ j = q_2 = -4.3 \mu C ]
- [ k = q_3 = q_4 3.6 \mu C ]
- [F_{ij} > 2F_{kj} ]
- Let: