-
Notifications
You must be signed in to change notification settings - Fork 51
prelecture_08_capacitors
- Parallel-Plate Capictor
- Discuss what happens when we insert a dielectric
- Prallel and Series Combination of capacitors
-
Last time
- [C \equiv \frac{ Q}{ \Delta V} = \frac{ Q}{ Ed} = \frac{ Q}{ \frac{ \sigma}{ \varepsilon_0} d} = \frac{ Q}{ \frac{ Q}{ \varepsilon_0 A} d} = \frac{ \varepsilon_0 A}{ d}]

- [C \equiv \frac{ Q}{ \Delta V} = \frac{ Q}{ Ed} = \frac{ Q}{ \frac{ \sigma}{ \varepsilon_0} d} = \frac{ Q}{ \frac{ Q}{ \varepsilon_0 A} d} = \frac{ \varepsilon_0 A}{ d}]
-
if [d] increases
- [Q] remains constant
- [E = \frac{ \sigma}{ \varepsilon_0}] remains constant
- [\Delta V = - \int{ \vec E \cdot d \vec l} = E d] increases
- [C = \frac{ Q}{ \Delta V} = \frac{ \varepsilon_0 A}{ d}] decreases
- [U] increases
- [W_{byField}] is negative
- [\Delta U = - W_{byField}] is positve
Two parallel plates have length [a] and width [b] and are separated by [a] distance [d] (which is much smaller than [a] and [b]). If all of the dimensions are doubled, how does the capacitance of the system change?

- The capacitance increases by a factor of 2
- The capacitance of a parallel-plate system is proportional to the area of the plates divided by the distance between them, which in this case equals [\frac{ a b}{ d}]. If [a], [b] and [d] are all doubled this becomes [ \frac{ 2 a 2 b}{ 2d} = \frac{ 2 a b}{ d}], which is twice as big as before.
-
So far we have discussed two types of materials
- Conductors
- Electrons are free to move
- Insulators
- Electrons do not move
- Conductors
-
Dielectric
- An insulating material in which the distribution of the charges within individual molecules is able to be modified by an applied electric field.
- By inserting a dielectric material between the plates of
a capacitor you end up with
- [E] decreases
- [V] decreases
- [C] increases
- The factor by which the capacitance increases is called the
dielectric constant.
- [C_{new} = \kappa C_{original}]
Two parallel plates are separated by a gap [d_0] filled with a dielectric material having [\kappa = 2]. Suppose you remove the dielectric material and you also change the spacing of the plates to a new value [d_1] such that the capacitance of the device remains the same.
How does [d_1] compare to [d_0]?

- [d_1 = \frac{ d_0}{ 2}]
- Removing the dielectric reduces the capacitance by a factor of 2. To increase this back to its original value, the spacing between the plates must be decreased by the same factor of 2.
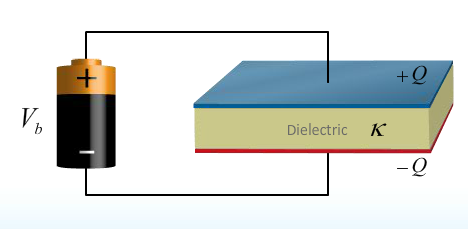
- Dielectric Added
- [C = \kappa C_0] increases
- The reason we added the dielectric in the first place
- [V_C = V_b] remains constant
- [Q = V_C C ]
- [U = \frac{ 1}{ 2} Q V_C] increases
- All energy must be provided by the battery
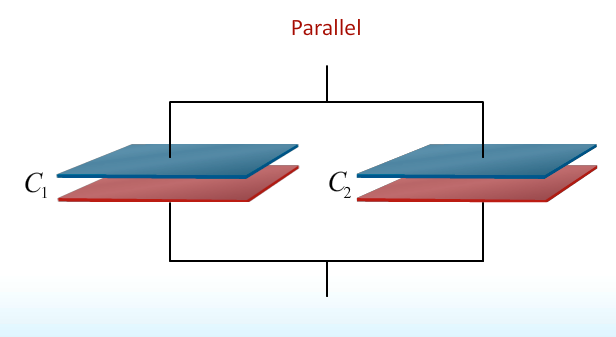
- [C = \kappa C_0] increases
- [V_{equivalent} = V_1 = V_2]
- [C_{equivalent} = C_1 + C_2]
- [C_{equivalent} = \frac{ \varepsilon_0 A_{equivalent}}{ d} = \frac{ \varepsilon_0 (A_1 + A_2)}{ d} = C_1 + C_2]
- [Q_{equivalent} = Q_1 + Q_2]
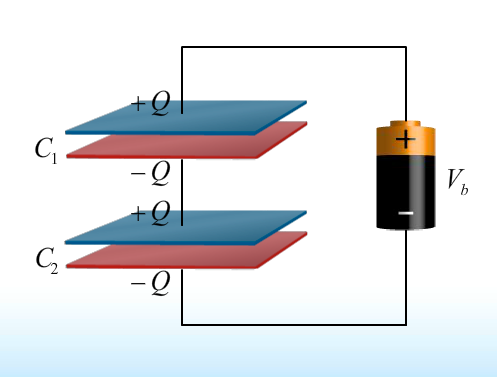
- Capacitors in Series
- [Q_{equivalent} = Q_1 = Q_2]
- [V_{equivalent} = V_1 + V_2]
- [\frac{ 1}{ C_{equivalent}} = \frac{ 1}{ C_1} + \frac{ 1}{ C_2}]
- [\frac{ 1}{ C_{equivalent}} = \frac{ 1}{ C_1} + \frac{ 1}{ C_2} \equiv \frac{ Q_{equivalent}}{ C_{equivalent}} = \frac{ Q_1}{ C_1} + \frac{ Q_1}{ C_2}]
- [\frac{ 1}{ C_{equivalent}} = \frac{ d_1}{ \varepsilon_0 A } \frac{ d_2}{ \varepsilon_0 A} = \frac{ 1}{ C_1} + \frac{ 1}{ C_2}]
Suppose you have two identical capacitors, each having capacitance [C]. [C_{max}] is the biggest possible equivalent capacitance that can be made by combining these two, and [C_{min}] is the smallest.
How does [C_{max}] compare to [C_{min}]?
- [C_{max} = 4 C_{min}]
- [C_{max}] is made by hooking the capacitors up in parallel, so [C_{max} = 2C]. [C_{min}] is made by hooking the capacitors up in series, so [\frac{ 1}Cmin = [frac{ 1}{ C} + \frac{ 1}{ C}], which we solve to find [C_{min} = \frac{ C}{ 2}]. [C_{max}] is therefore four times as big as [C_{min}].